PAT (Basic Level) Practice题解 1007 素数对猜想 [C语言实现]

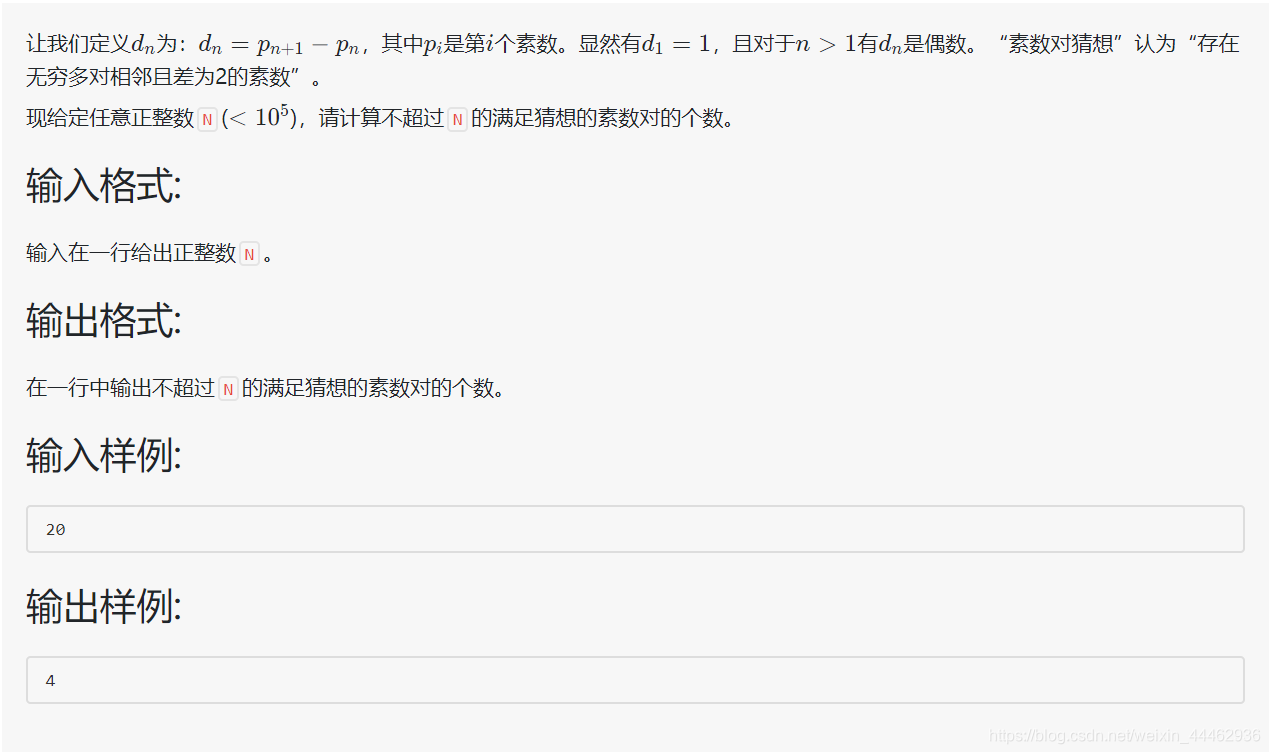
题目

原题链接

思路

• 问题
  素数判定，按照原来的思路，判断x是否是素数，用x除以所有小于自身的正整数（不含1），如果不能被整除，即是素数。但这种思路代码实现会导致超时不通过
• 改进

  • 方案1：⽆无须到x-1，到sqrt(x)就够了(平方根)

  • 方案2：建立素数表，x除以比自己小的素数就能判定了

  • 两种方案都能通过，不超时

本题用方案1，省事，具体的代码实现方式看注释吧

代码

#include <stdio.h>

int main()
{
    int n;//输入正整数N
    //声明临时数组，轮流存储相邻的两个素数，初始化tmp[0]=3,然后从5开始数
    int tmp[2] = {3};   
    int cnt = 0;//孪生素数计数
    scanf("%d",&n);
    for(int i = 5; i <= n; i++)//从5开始，直到n(包括)
    {
        int flag = 1;//标记是否为素数
        for(int j = 2; j * j <= i; j++)//循环条件用j < i的话会超时，只要验证到平方即可
        {
            if(i % j == 0)//如果能被整除，flag = 0,非素数
            {
				flag = 0;
            	break;//跳出循环
        	}
        }       
        if(flag)//如果当前i是素数
        {
            tmp[1] = i;//tmp[1]记录dn，tmp[0]记录dn-1
            if( tmp[1] - tmp[0] == 2)//相邻差为2，计数就+1
				cnt++;
            tmp[0] = tmp[1];//为记录下一个素数，覆盖掉先前的数据
        }       
    }
    printf("%d",cnt);
    return 0;
}

欢迎指正