局部最优-------> 全局最优
只顾眼前利益
排序,贪心的前提
1.活动安排问题

题目
“今年暑假不AC?”
“是的。”
“那你干什么呢?”
“看世界杯呀,笨蛋!”
“@#$%^&*%…”
确实如此,世界杯来了,球迷的节日也来了,估计很多ACMer也会抛开电脑,奔向电视了。
作为球迷,一定想看尽量多的完整的比赛,当然,作为新时代的好青年,你一定还会看一些其它的节目,比如新闻联播(永远不要忘记关心国家大事)、非常6+7、超级女生,以及王小丫的《开心辞典》等等,假设你已经知道了所有你喜欢看的电视节目的转播时间表,你会合理安排吗?(目标是能看尽量多的完整节目)
Input
输入数据包含多个测试实例,每个测试实例的第一行只有一个整数n(n<=100),表示你喜欢看的节目的总数,然后是n行数据,每行包括两个数据Ti_s,Ti_e (1<=i<=n),分别表示第i个节目的开始和结束时间,为了简化问题,每个时间都用一个正整数表示。n=0表示输入结束,不做处理。
Output
对于每个测试实例,输出能完整看到的电视节目的个数,每个测试实例的输出占一行。
Sample Input
12 //12个样例
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0 //当输入样例个数为0 是程序运行结束
Sample Output
5
贪心策略
1.最早开始时间。
2.最早结束时间。 !!!
3.用时最少。
#include<iostream>
#include<cstdio>
#include <algorithm>
using namespace std;
struct node{
int end,start; //活动结束时间和开始时间
};
bool cmp(const node &p,const node &q){
return p.end < q.end; //活动结束时间早的排在前面
}
int main(){
int n;
while(cin >>n && n){ // 输入n个活动 && n 当n = 0程序结束
node a[101]; //每次数组a要清零
for(int i=0;i<n;i++){
cin >> a[i].start >> a[i].end;
}
sort(a,a+n,cmp); //按结束时间排序
int ans=0;
int last=-1; //给一个小值
for(int i=0;i<n;i++){ //贪心算法
if(a[i].start>=last){ //后一个起始时间大于等于 前一个终止时间
ans++;
last=a[i].end; //记录前一个活动的终止时间
}
}
cout <<ans <<endl; //输出活动次数
}
return 0;
}
2.区间覆盖问题
3.最优装载问题

题目大意
有n种药水,体积都是V,浓度不同,把它们混合起来,得到浓度不大于w%的药水,问怎么混合才能得到最大体积的药水?注意一种药水要么全用,要么不用。
Input
输入数据的第一行是一个整数C,表示测试数据的组数;
每组测试数据包含2行,首先一行给出三个正整数n,V,W(1<=n,V,W<=100);
接着一行是n个整数,表示n种药水的浓度Pi%(1<=Pi<=100)。
Output
对于每组测试数据,请输出一个整数和一个浮点数;
其中整数表示解药的最大体积,浮点数表示解药的浓度(四舍五入保留2位小数);
如果不能配出满足要求的的解药,则请输出0 0.00。
Sample Input
3
1 100 10
100
2 100 24
20 30
3 100 24
20 20 30
Sample Output
0 0.00
100 0.20
300 0.23
1.当药水浓度小于给定的浓度,直接加
2.当药水浓度大于给定的浓度,算加上去浓度有没有超标
#include<iostream>
#include<cstdio>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
int main(){
int t,n,v,w;
cin >>t;
while(t--){
int a[1001];
cin >>n>>v>>w;
for(int i=0;i<n;i++){
cin >>a[i];
}
sort(a,a+n);
int v1=0,n1=0;
double r1=0;
for(int i=0;i<n;i++){
if(a[i]<w){
v1++; //巧妙运用每种药水不同浓度,相同体积
r1+=a[i];
}else{
if(1.0*(r1+a[i])/(v1+1)>w){
break;
}
else{
v1++;
r1+=a[i];
}
}
}
if(r1==0){
printf("%d 0.00\n",v1);
}
else printf("%d %.2f\n",v1*v,r1/v1/100);
}
return 0;
}
4.多机调度问题
5.Huffman编码

An entropy encoder is a data encoding method that achieves lossless data compression by encoding a message with “wasted” or “extra” information removed. In other words, entropy encoding removes information that was not necessary in the first place to accurately encode the message. A high degree of entropy implies a message with a great deal of wasted information; english text encoded in ASCII is an example of a message type that has very high entropy. Already compressed messages, such as JPEG graphics or ZIP archives, have very little entropy and do not benefit from further attempts at entropy encoding.
English text encoded in ASCII has a high degree of entropy because all characters are encoded using the same number of bits, eight. It is a known fact that the letters E, L, N, R, S and T occur at a considerably higher frequency than do most other letters in english text. If a way could be found to encode just these letters with four bits, then the new encoding would be smaller, would contain all the original information, and would have less entropy. ASCII uses a fixed number of bits for a reason, however: it’s easy, since one is always dealing with a fixed number of bits to represent each possible glyph or character. How would an encoding scheme that used four bits for the above letters be able to distinguish between the four-bit codes and eight-bit codes? This seemingly difficult problem is solved using what is known as a “prefix-free variable-length” encoding.
In such an encoding, any number of bits can be used to represent any glyph, and glyphs not present in the message are simply not encoded. However, in order to be able to recover the information, no bit pattern that encodes a glyph is allowed to be the prefix of any other encoding bit pattern. This allows the encoded bitstream to be read bit by bit, and whenever a set of bits is encountered that represents a glyph, that glyph can be decoded. If the prefix-free constraint was not enforced, then such a decoding would be impossible.
Consider the text “AAAAABCD”. Using ASCII, encoding this would require 64 bits. If, instead, we encode “A” with the bit pattern “00”, “B” with “01”, “C” with “10”, and “D” with “11” then we can encode this text in only 16 bits; the resulting bit pattern would be “0000000000011011”. This is still a fixed-length encoding, however; we’re using two bits per glyph instead of eight. Since the glyph “A” occurs with greater frequency, could we do better by encoding it with fewer bits? In fact we can, but in order to maintain a prefix-free encoding, some of the other bit patterns will become longer than two bits. An optimal encoding is to encode “A” with “0”, “B” with “10”, “C” with “110”, and “D” with “111”. (This is clearly not the only optimal encoding, as it is obvious that the encodings for B, C and D could be interchanged freely for any given encoding without increasing the size of the final encoded message.) Using this encoding, the message encodes in only 13 bits to “0000010110111”, a compression ratio of 4.9 to 1 (that is, each bit in the final encoded message represents as much information as did 4.9 bits in the original encoding). Read through this bit pattern from left to right and you’ll see that the prefix-free encoding makes it simple to decode this into the original text even though the codes have varying bit lengths.
As a second example, consider the text “THE CAT IN THE HAT”. In this text, the letter “T” and the space character both occur with the highest frequency, so they will clearly have the shortest encoding bit patterns in an optimal encoding. The letters “C”, "I’ and “N” only occur once, however, so they will have the longest codes.
There are many possible sets of prefix-free variable-length bit patterns that would yield the optimal encoding, that is, that would allow the text to be encoded in the fewest number of bits. One such optimal encoding is to encode spaces with “00”, “A” with “100”, “C” with “1110”, “E” with “1111”, “H” with “110”, “I” with “1010”, “N” with “1011” and “T” with “01”. The optimal encoding therefore requires only 51 bits compared to the 144 that would be necessary to encode the message with 8-bit ASCII encoding, a compression ratio of 2.8 to 1.
Input
The input file will contain a list of text strings, one per line. The text strings will consist only of uppercase alphanumeric characters and underscores (which are used in place of spaces). The end of the input will be signalled by a line containing only the word “END” as the text string. This line should not be processed.
Output
For each text string in the input, output the length in bits of the 8-bit ASCII encoding, the length in bits of an optimal prefix-free variable-length encoding, and the compression ratio accurate to one decimal point.
Sample Input
AAAAABCD
THE_CAT_IN_THE_HAT
END
Sample Output
64 13 4.9
144 51 2.8
大致翻译
输入一个字符串,分别用普通ASCII编码(每个字符8bit)和Huffman编码,输出编码后的长度,并输出压缩比。END程序结束
#include<string>
#include<cstdio>
#include<cstring>
#include<stdlib.h>
#include<algorithm> //用这个头文件就是不行#include<bits/stdc++.h>
#include<queue>
#include<iostream>
using namespace std;
const int N=1000+5;
int main(){
string s;
priority_queue< int,vector<int>,greater<int> >q; //优先队列q从大到小排序
while(getline(cin,s)){
if(s=="END")break;
sort(s.begin(),s.end()); //字符串里的字符进行从小到大排序
int t=1;
int x=s.length();
for(int i=1;i<x;i++){
if(s[i]!=s[i-1]){
q.push(t); //计算每个字符个数入队
t=1;
}
else t++;
}
q.push(t);
int ans=0;
int t1,t2;
if(q.size()==1){ //这个很重要
ans=x;
}
else{
while(q.size()>1){
t1=q.top();q.pop();
t2=q.top();q.pop();
q.push(t1+t2);
ans+=t1+t2;
}
}
q.pop(); //清空优先队列q
x=x*8;
float w=(1.0*x)/(ans*1.0);
printf("%d %d %.1f\n",x,ans,w);
}
return 0;
}

在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1,
并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
例如有3种果子,数目依次为1,2,9。可以先将 1、2堆合并,新堆数目为3,耗费体力为3。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为12,耗费体力为 12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
输入
输入包括两行,第一行是一个整数n(1 <= n <= 10000),表示果子的种类数。第二行包含n个整数,用空格分隔,第i个整数ai(1 <= ai <= 20000)是第i种果子的数目。
输出
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。输入数据保证这个值小于2310。
样例输入 Copy
3
1 2 9
样例输出 Copy
15
提示
对于30%的数据,保证有n <= 1000;
对于50%的数据,保证有n <= 5000;
对于全部的数据,保证有n <= 10000。
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 10005
using namespace std;
priority_queue<int>q;
int main()
{
int n,i,x,t,ans=0;
scanf("%d",&n);
for(i=1;i<=n;++i)
{
scanf("%d",&x);
q.push(-x); //priority_queue< int,vector<int>,greater<int> >q;想要得到的结果一样,注释这个更好。两题方法差不多
}
while(--n)
{
t=0;
t-=q.top();q.pop();
t-=q.top();q.pop();
ans+=t;
q.push(-t);
}
printf("%d",ans);
return 0;
}
6.模拟退火(近似值)

Now, here is a fuction:
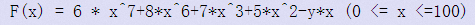
!!! (0 <= x <=100)
Can you find the minimum value when x is between 0 and 100.
Input
The first line of the input contains an integer T(1<=T<=100) which means the number of test cases. Then T lines follow, each line has only one real numbers Y.(0 < Y <1e10)
Output
Just the minimum value (accurate up to 4 decimal places),when x is between 0 and 100.
Sample Input
2
100
200
Sample Output
-74.4291
-178.8534
#include<iostream>
#include<cstdio>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8; //终止温度
double y;
double func(double x){ //计算函数
return 6*pow(x,7.0)+8*pow(x,6.0)+7*pow(x,3.0)+5*pow(x,2.0)-y*x;
}
double solve(){
double T=100; //初始温度
double del = 0.98; //降温系数 自己定义的数,小精确但是运行时间长
double x=50.0; //x的初始值
double now =func(x); //计算函数的值
double ans =now; //返回值
while(T>eps){
int f[2]={1,-1};
double newx = x+f[rand()%2]*T; //按概率改变x,随Td降温而减少
if(newx>=0 && newx<=100){
double next = func(newx);
ans = min(ans,next);
if(now - next>eps){
x = newx;now = next; //更新x
}
}
T*=del;
}
return ans;
}
int main(){
int cas;
scanf("%d",&cas);
while(cas--){
scanf("%lf",&y);
printf("%.4f\n",solve());
}
return 0;
}























 423
423

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








