螺旋矩阵

从左上角填上 1 开始，顺时针方向依次填入数字
1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7

大一的时候助教出的这道题目，当时我感觉好难呀，这是人做的题目嘛？，那时刚学二维数组，对这道题目手足无措，也是想了好久才想出来。最近刷题还能碰到这个题目，以及变形题目，看来这个题还是比较普遍的，那么今天就写一下题解。

题目倒是很好理解呀，就是顺时针从外到内填数。思考一下我们肯定是不可能边赋值边输出的，那么我们就得建立一个二维数组存一下每个位置的数。我们看一下以输入4为例的结果(上面有)：
我们肯定是分成4个组来进行赋值的：
左上→右上
↑ 、、、 ↓
左下←右下
我们就先看外面最后一层，会发现其实每组只赋值3个元素就行，这个的意思就是:
左上到右上进行第1行第1-3列的赋值 1 2 3
右上到右下进行第4列第1-3行的赋值 4 5 6
右下到左下进行第4行第4-2列的赋值 7 8 9
左下到左上进行第1列第4-2行的赋值 10 11 12

1	2	3		4
	–	–	–	5
12	–	–	–	6
11	–	–	–
10	–	9	8	7

因此我们就可以发现转一圈正好形成一个闭环，第二层的话再形成一个闭环，一直到值为4*4结束，然后打印二维数组即可。

#include<bits/stdc++.h>
using namespace std;
int a[10][10];//每个点的值的为0
int main(){
    int n,ans=1;
    int x=1,y=1;
    scanf("%d",&n);
    a[x][y]=1;
    while(n*n>ans){
    
    	//这里解释一下!a[x][y+1]，以左上到右上为例
    	//y<n是用来控制外围的范围的，也就是最外圈
    	//我们外层了值以后执行第二层的话，最外层的已经赋上大于0的值
    	//我们碰到大于0的数就说明走到“头”了，就跳出循环
    	//例如n=4，我们已经走完外圈，走里圈的话，走到了【2，3】的位置
    	//发现【2，4】已经有值了，我们就跳出循环，开始往下走
    	
        while(y<n&&!a[x][y+1]){//左上到右上
            a[x][y++]=ans++;
        }
        while(x<n&&!a[x+1][y]){//右上到右下
            a[x++][y]=ans++;
        }
        while(y>1&&!a[x][y-1]){//右下到左下
            a[x][y--]=ans++;
        }
        while(x>1&&!a[x-1][y]){/左下到左上
            a[x--][y]=ans++;
        }
    }
    a[x][y]=ans;//由于ans是从1开始的，
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            printf("%3d",a[i][j]);//占3个字符右对齐输出
        }
        puts("");//相当于回车
    }
    return 0;
}

洛谷有原题👇，大家可以在洛谷的评测机上进行测评
螺旋矩阵题目

有兴趣的童鞋可以看看这个题目的变式👇

做过上面的题目就会发现数据很小呀，那么如果数据大一些，让我们求某个位置的值怎么办呢？
以这个题目为例👇题目链接
https://www.luogu.com.cn/problem/P2239
很明显题目给出的数据很大，如果还是按上面的做法写的话，我们分析一下时间复杂度，O(n²)带入数据的话是9e8,评测机1s内跑的数据也就是在1e8左右，所以这种方法肯定是不行的。
通常的话，这个类型的题目都是可以求出递推式或者公式能够很快的求出答案。
我们上面的推导就是把这个矩阵分成一个圈一个圈的，这个题目上面题目的变形，推导应该也是类似的，我们不妨先把图画出来观察一下。
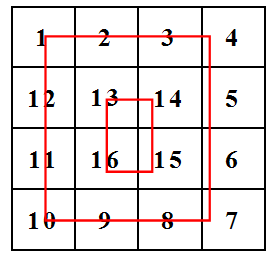
n=4的情况

n=6的情况

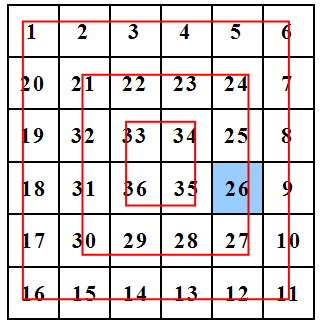
算层数：
简单观察下我们就能发现 i，j在矩阵的第几层就是i，j，n+1-i，n+1-j中最小的那一值
这里我们就能够得到圈数：q=min(x, y, n-x+1, n-y+1 )

算所求层的起点：
第k层的起点是上一层的起点加上上一圈边长减1的4倍；
F(k)=F(k-1)+4(n-1-2×(k-1))
F(1)=1;
推导可得通项式:F(k)=1+4(k-1)(n-k+1)

算(i,j)离(k,k)的距离：

如果所求i,j在矩阵上半的三角
直接加i-k+j-k即可;

在下半个三角的时候
我们可以把k的对角点当新的起点,也就是算（i，j）到(k+(n-1-2*(k-1)),k+(n-1-2*(k-1)))的距离

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n, i, j, ans;
    cin >> n >> i >> j;
    int cen = min(min(min(i, j), (n - i + 1)), (n - j + 1)); //算第几层
    ans = 4 * (cen - 1) * (n - cen + 1) + 1;                 //第cen层的起点
    if (i == n - cen + 1 || j == cen)                        //如果在下半部分
        ans += 2 * (n - 1 - 2 * (cen - 1)), cen += (n - 1 - 2 * (cen - 1));
    cout << ans + abs(i - cen) + abs(j - cen);
    return 0;
}