洛谷 P1548 棋盘问题

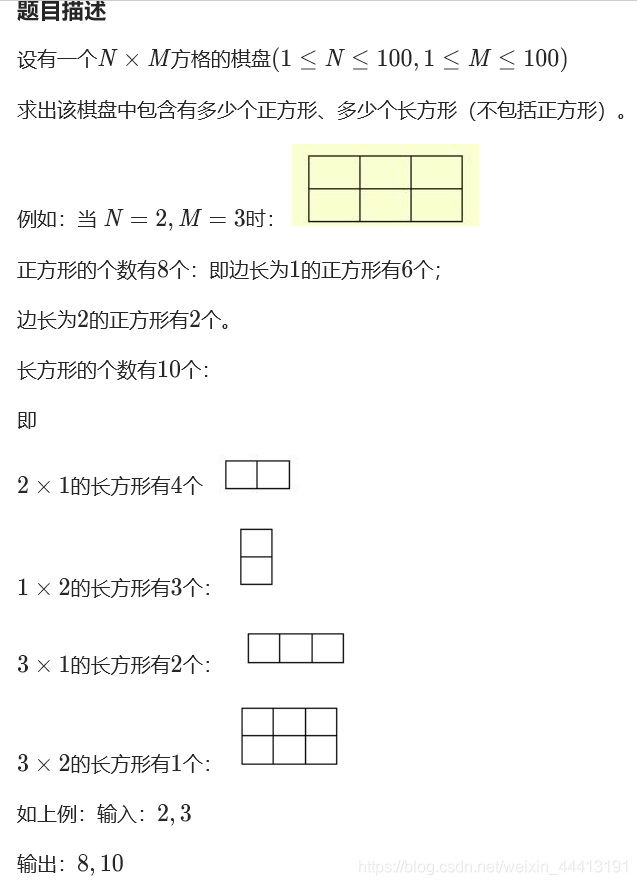
找规律：
正方形:
边长为1的正方形个数为nm
边长为2的正方形个数为(n-1)(m-1)
边长为3的正方形为个数(n-2)(m-2)
边长为min(n,m)的正方形为个数s1=(n-min(n,m)+1)(m-min(n,m)+1)
然后从边长为1到min（m，n）的正方形个数全部加起来；
长方形:(包括正方形)
长为1的长方形（包括正方形）有n个
长为2的长方形（包括正方形）有n-1个
长为n的长方形（包括正方形）有1个
长为1到n的长方形1+2+…+n个
同理
宽为1的长方形（包括正方形）有m个
宽为2的长方形（包括正方形）有m-1个
宽为m的长方形（包括正方形）有1个
宽为1-m的长方形1+2+…+m个
然后把它们乘起来，根据乘法原理，总数s2=((1+n)*(1+m)nm)/4;
题目要求的是“非正方形的长方形”，因此要减去cnt1;

#include<bits/stdc++.h>
using namespace std;
int main()
{
 int n, m, i; cin >> n >> m;
 int cnt1 = 0, cnt2 = 0;
 int a = n, b = m;//用a,b记录m,n，否则m,n值会在for循环中改变
 for (i = 0; i < min(m, n); i++) {
  cnt1 += a * b;
  a--;
  b--;
 }
 cnt2 = (1 + n) * (1 + m) * n * m / 4 - cnt1;
 cout << cnt1 << " " << cnt2;
 return 0;
}