本文详细介绍了四个积分环节的应用实例，涉及不同频率和初始条件下的sin函数输入，包括了Simulink中对应的时域分析，展示了积分环节的延迟和幅值变化。核心内容包括积分环节的1/s转换及Bode图解析，频率最大输出趋近于0的特性。
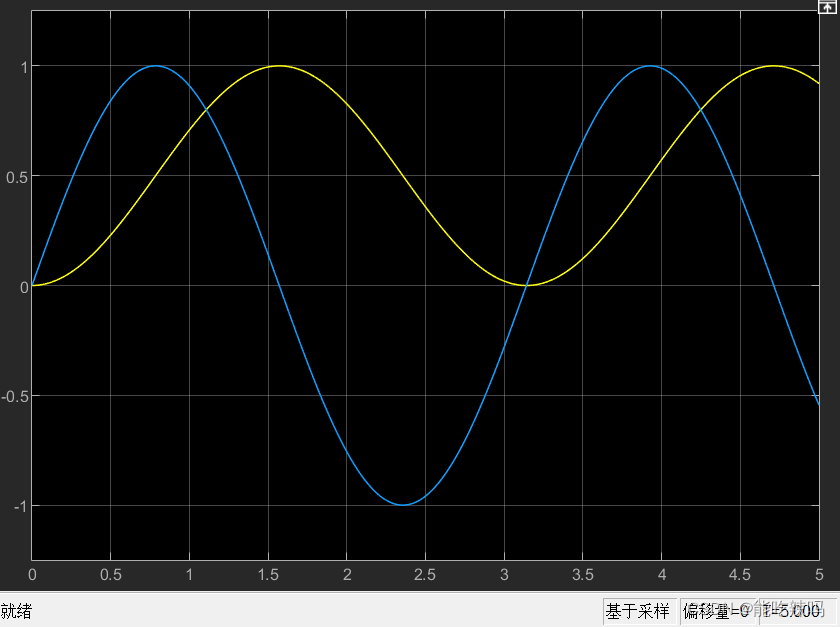
Example 1
输入是
sin
(
2
t
)
\sin(2t)
sin(2t)，初始值为0的积分环节是
1
s
\frac{1}{s}
s1，simulink是
时域分析（蓝色为积分环节输入，黄色为积分环节输出）：延迟
π
2
\frac{\pi}{2}
2π，幅值比例
1
2
\frac{1}{2}
21
Example 2
输入是
sin
(
5
t
)
\sin(5t)
sin(5t)，初始值为0的积分环节是
1
s
\frac{1}{s}
s1，simulink是
时域分析（蓝色为积分环节输入，黄色为积分环节输出）：延迟
π
2
\frac{\pi}{2}
2π，幅值比例
1
5
\frac{1}{5}
51
Example 3
输入是
sin
(
5
t
)
\sin(5t)
sin(5t)，初始值为
−
0.2
-0.2
−0.2 的积分环节是
1
s
\frac{1}{s}
s1，simulink是
时域分析（蓝色为积分环节输入，黄色为积分环节输出）：延迟
π
2
\frac{\pi}{2}
2π，幅值比例
1
5
\frac{1}{5}
51
Example 4
输入是 sin ( 50 t ) \sin(50t) sin(50t)，初始值为 − 0.02 -0.02 −0.02 的积分环节是 1 s \frac{1}{s} s1，simulink是
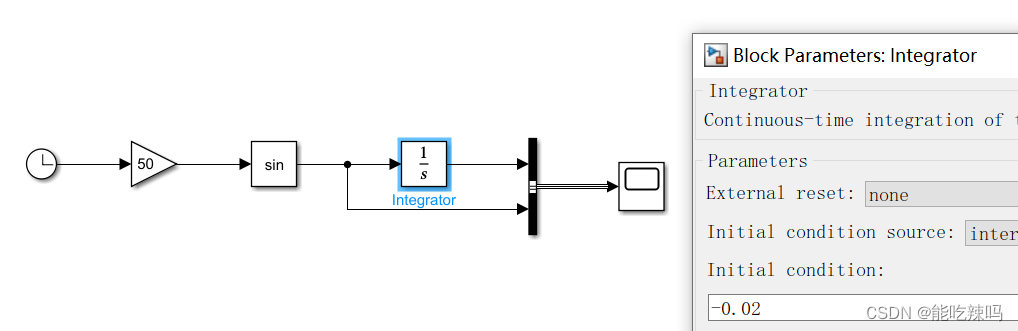
时域分析（蓝色为积分环节输入，黄色为积分环节输出）：延迟
π
2
\frac{\pi}{2}
2π，幅值比例
1
50
\frac{1}{50}
501
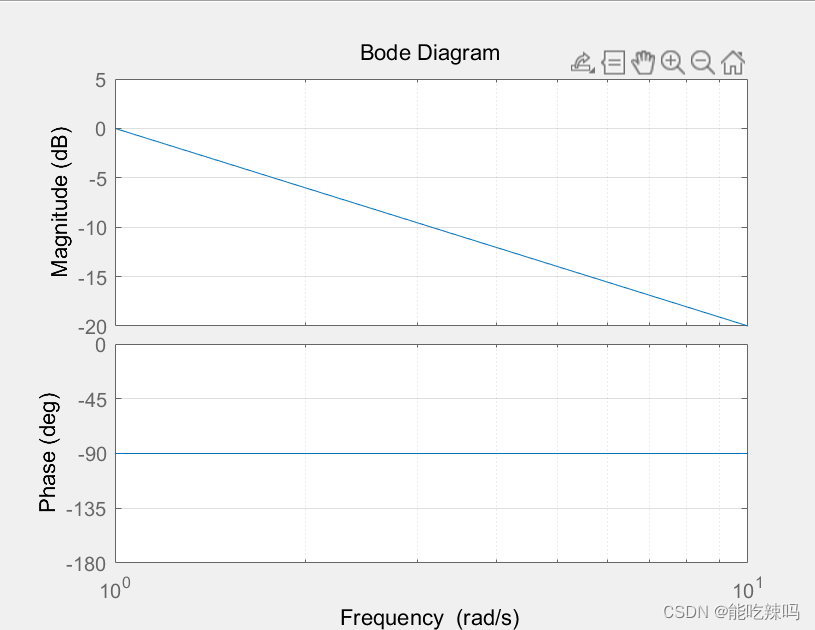
频域
积分环节
1
s
\frac{1}{s}
s1的Bode图，随着频率最大，积分环节输出幅值趋向于0。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
