20220712 根轨迹的一个例子_g(s)= k(0.05s+1)s(0.0714s+1)(0.012s2 + 0.1s +1)的根轨-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_44382195/article/details/125745580

本文详细介绍了根轨迹的概念及其在控制系统分析中的应用，通过多个实例展示了如何利用MATLAB的rlocus函数绘制根轨迹，并探讨了不同参数对系统稳定性的影响。这些例子从简单的系统开始，逐步增加复杂性，帮助读者深入理解根轨迹法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

例1
例2
例3
例4
例5

根轨迹是开环系统某一参数从零变到无穷时，闭环系统特征方程式的根在s平面上变化的轨迹。根轨迹是分析和设计线性定常控制系统的图解方法，使用十分简便，特别在进行多回路系统的分析时，应用根轨迹法比用其他方法更为方便，因此在工程实践中获得了广泛应用。胡寿松．自动控制原理．北京：科学出版社，2007年第五版：144-159

注：这里所说的开环传函包含单位反馈中的G，和非单位反馈中的GH

例1

开环传函为 $G=\frac{1}{s(s+6)((s+5)^2+3^2)}$ 开环极点4个： $s = 0, s = - 6, s = - 5 + 3 i, s = - 5 - 3 i$ matlab代码为

s = tf('s');
G = 1/(s*(s+6)*((s+5)^2+3^2));
rlocus(G);
axis equal;

图像为
在这里插入图片描述

例2

开环传函为 $G=\frac{1}{s(s+6)((s+4)^2+3^2)}$ 开环极点4个： $s = 0, s = - 6, s = - 4 + 3 i, s = - 4 - 3 i$ matlab代码为

s = tf('s');
G = 1/(s*(s+6)*((s+4)^2+3^2));
rlocus(G);
axis equal;

图像为
在这里插入图片描述

例3

开环传函为 $G=\frac{1}{s(s+6)((s+3)^2+3^2)}$ 开环极点4个： $s = 0, s = - 6, s = - 3 + 3 i, s = - 3 - 3 i$ matlab代码为

s = tf('s');
G = 1/(s*(s+6)*((s+3)^2+3^2));
rlocus(G);
axis equal;

图像为
在这里插入图片描述

例4

开环传函为 $G=\frac{1}{s(s+6)((s+2)^2+3^2)}$ 开环极点4个： $s = 0, s = - 6, s = - 2 + 3 i, s = - 2 - 3 i$ matlab代码为

s = tf('s');
G = 1/(s*(s+6)*((s+2)^2+3^2));
rlocus(G);
axis equal;

图像为
在这里插入图片描述

例5

开环传函为 $G=\frac{1}{s(s+6)((s+1)^2+3^2)}$ 开环极点4个： $s = 0, s = - 6, s = - 1 + 3 i, s = - 1 - 3 i$ matlab代码为

s = tf('s');
G = 1/(s*(s+6)*((s+1)^2+3^2));
rlocus(G);
axis equal;

图像为
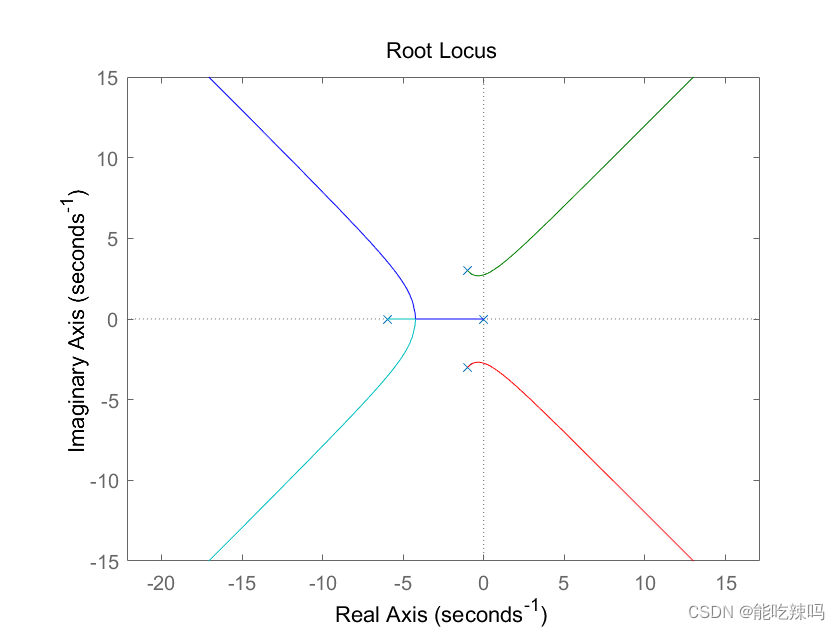
在这里插入图片描述