机器学习(二)之回归模型
回归模型
回归模型(Regression Model):是一种有监督学习算法,用来建立自变量X和观测变量Y之间的映射关系。若观测变量Y是连续的则属于回归模型,若Y是离散的是属于分类模型。
回归定义:找到一个函数,通过输入特征X,输出一个数值scalar。
应用举例:
股市预测:
输入:过去10年股票的变动、新闻咨询、公司并购咨询
输出:预测股市明天的平均值
自动驾驶:
输入:无人车的路况、测量的车距等
输出:方向盘的角度
Pokemon精灵攻击的预测:
输入:进化前的cp值、物种、血量(HP)、重量(weight)、高度(Height)等。
输出:进化后的cp值
线性回归模型步骤
step1:模型假设,选择模型框架(线性回归模型)
step2:模型评估,如何判断众多模型的好坏(损失函数)
step3:模型优化,如何筛选最优模型(梯度下降)
step1:模型假设——线性模型
(1)一元线性模型:单个特征

(2)多元线性模型:多个特征
在实际应用中,输入特征肯定不止 Xcp 这一个。例如,进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)等,特征会有很多。假设线性模型为y=b+∑WiXi,Xi表示各种特征值Xcp、Xhp、Xw、Xh,Wi表示各个特征的权重,b表示偏移量。
step2:模型评估——损失函数
[单个特征Xcp]
衡量模型的好坏从数学的角度就是看距离的长短,求[进化后的cp值]与[模型预测的cp值]之间的差来判定模型的好坏,也就是使用损失函数来衡量模型的好坏。统计10组原始数据,距离和越小说明误差越小,则模型越好。

step3:最佳模型——梯度下降
[单个特征值Xcp]


步骤1:随机选取一个 w^0
步骤2:计算微分,也就是当前的斜率,根据斜率来判定移动的方向
大于0向右移动(增加w)
小于0向左移动(减少w)
步骤3:根据学习率移动
重复步骤2和步骤3,直到找到最低点,此时L(w)最小。
在线性模型中使用梯度下降基本能找到最低点。
再从w和b两个参数入手分别求偏微分,寻找使L(w,b)值最小的w和b。


问题1:如果初始参数就处于最优呢
问题2:斜率等于0
问题3:斜率趋于0
选择其他更复杂的1元N次线性模型




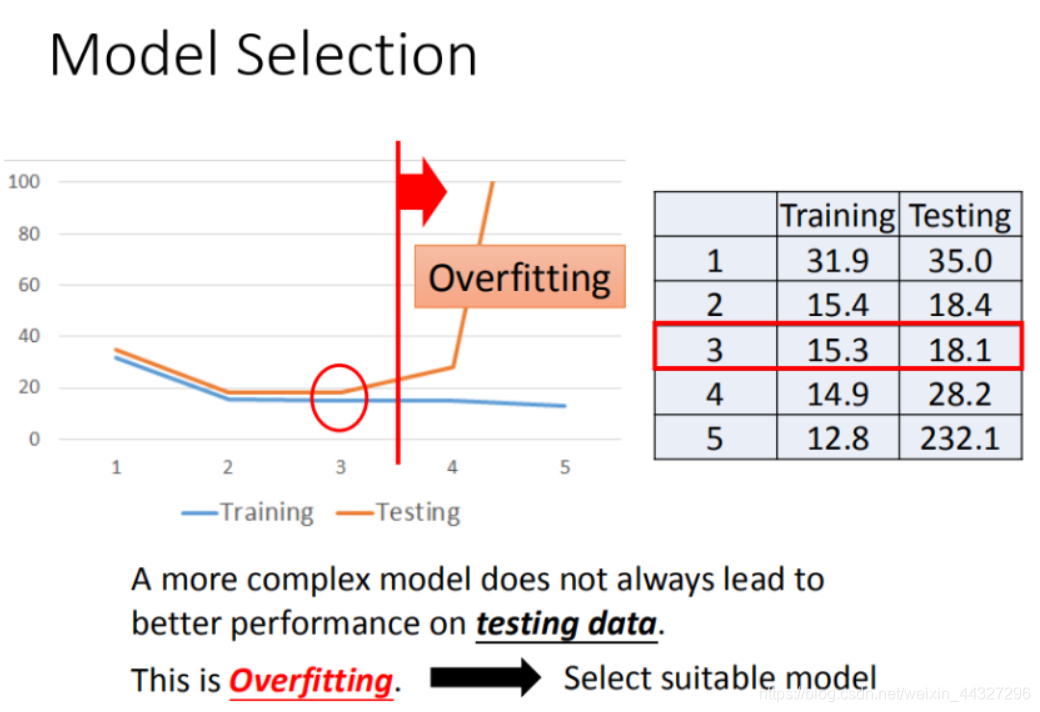 选择模型并不是越复杂越好,本次选择1元3次最合适。
选择模型并不是越复杂越好,本次选择1元3次最合适。
步骤优化
输入更多的数据后发现不同物种影响了进化后的cp值。
合并法
将4种物种不同的线性模型合并到一个线性模型中。
引入更多参数
在合并的基础上引入更多的参数,例如血量HP,高度Height,重量Weight。
正则化
引入更多特征后,权重w可能会使某些特征权重值过高,导致模型选择不合适,所以引入正则化。























 1447
1447

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








