多元线性回归算法预测房价

目录

一、线性回归理论基础

二、多元线性回归

1、针对房屋数据集“house_prices.csv”做多元线性回归（基于统计分析库statsmodels）

三、用Excel重做上面的多元线性回归，求解回归方程

四、用机器学习库Sklearn库重做上面的多元线性回归

五、三者的结果对比分析

六、总结

---

        garbage in garbage out”（简称GIGO），是计算机术语常用的俚语，意思是如果你输入错误的数据，那么（计算机）输出的结果也是错误的。这个结论在机器学习领域也成立。多元线性回归属于监督机器学习算法，通过已知数据训练得到模型或决策函数。应用此算法时，不能盲目地套用算法，必须对数据的有效性、正确性、假设合理性进行验证，如果发现数据本身不正确，就需要纠正。多元线性回归适用于对受到多因素影响的数据进行分析的场景。由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。

一、线性回归理论基础

        一元线性回归分析是只有一个自变量（自变量x和因变量y）线性相关关系的方法。一个经济指标的数值往往受许多因素影响，若其中只有一个因素是主要的，起决定性作用，则可用一元线性回归进行预测分析。一元线性回归分析的数学模型为：

        其中，是自变量的值；

        是因变量的值；

        a、b是代表一元线性回归方程的参数。

        a、b参数由下列公式可求得：

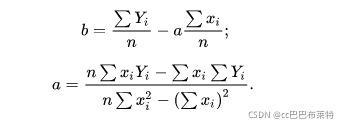
        多元线性回归分析中的因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归亦称多重回归。当自变量与因变量之间是线性关系时，所进行的回归分析就是多元线性回归。设为因变量，为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

        其中，为常数项，为回归系数，为固定时，每增加一个单位对的效应，即对的偏回归系数；同理，为固定时，每增加一个单位对的效应，即对的偏回归系数 ，等等。如果两个自变量、同一个因变量呈线性相关时，可用二元线性回归模型描述为：

         建立多元线性回归模型时，为了保证回归模型具有优良的解释能力和预测效果，应首先注意自变量的选择，其准则是：

(1)自变量对因变量必须有显著的影响，并呈密切的线性相关；

(2)自变量与因变量之间的线性相关必须是真实的，而不是形式上的；

(3)自变量之间应具有一定的互斥性，即自变量之间的相关程度不应高于自变量与因变量之间的相关程度；

(4)自变量应具有完整的统计数据，其预测值容易确定。

        多元线性回归模型的参数统计，同一元线性回归方程的一样，也是在要求误差平方和为最小的前提下，用最小二乘法求解参数。以二元线性回归模型为例，求解回归方程参数的标准方程组为：

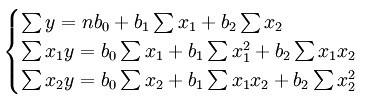
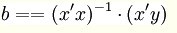
 解此方程可求得的值，亦可以通过下列矩阵法求得：

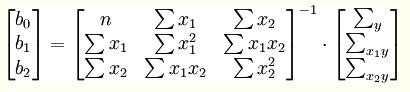
 回归性能好坏使用均方误差(Mean Squared Error)MSE进行评估，评估机制：