方差分析
Gamma公式展示
Γ
(
n
)
=
(
n
−
1
)
!
∀
n
∈
N
\Gamma(n) = (n-1)!\quad\forall n\in\mathbb N
Γ(n)=(n−1)!∀n∈N 是通过 Euler integral
Γ
(
z
)
=
∫
0
∞
t
z
−
1
e
−
t
d
t
.
\Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt\,.
Γ(z)=∫0∞tz−1e−tdt.
因素是：moreQJ moreSJ lessQJ lessSJ——一定是分类变量
特征值：up_score的均值，是否有显著的区别—— 一定是连续变量
只要有一个不相等就拒绝原假设
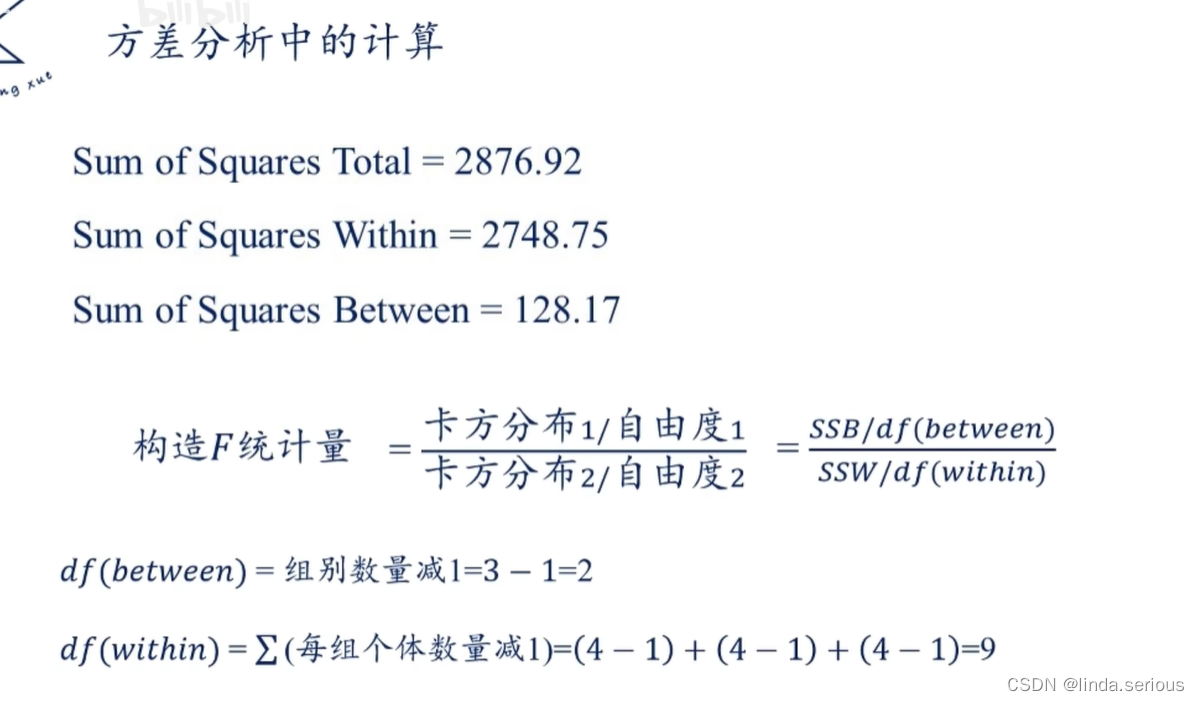
sst=ssw+ssb
双因素方差分析
我们的特征值是不是受到2个因素的影响？
5个波动
模型所带来的波动就是2个因素可以解释的波动（不管是主效应还是交互效应）
模型不能解释的，2个因素不能解释的–误差波动（除了案例和教育方式之外的，比如性别、年龄等等）
检验思路
如果more的波动显著大于 误差项的波动，我们就说因素一对整体的波动是有影响的，也就是因素一more对特征值教育效果是有影响的
自由度
上图分母都是误差项的SS
F统计量对应的P值，如果小于0.05，就说明该因素有显著的影响
扫一扫
5699
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
