蓝桥杯剪邮票全排列加DFS

剪邮票

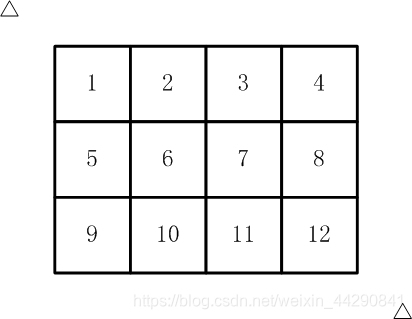
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
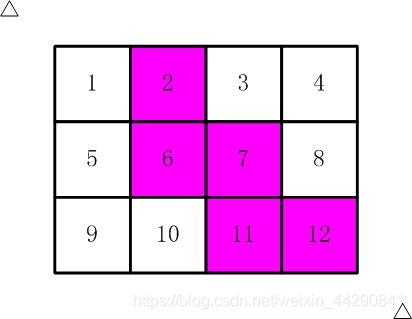
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。
 

 

第一次看到这个题，以为是纯粹的深搜，后来发现答案不对，一个很重要的原因是它不能够检测形如T字形图案，例如

 先展示一下错误代码，毕竟敲出来也不容易，顺便给自己加深印象

正确代码在最下面

#include<iostream>
#include<string>
#include<set>
#include<algorithm>
using namespace std;

set<string> my_set;
int num = 0;
bool state[12];
string str = "0123456789ab";
void dfs(int d, int p)
{
	state[p] = true;
	if(d==4)
	{
		string s;
		for(int i=0;i<=11;++i)
			if(state[i])
				s+=str[i];
		my_set.insert(s);
		++num;
		state[p] = false;
		return;
	}
	if(p-4>=0 && !state[p-4])
		dfs(d+1,p-4);
	if(p%4!=0 && p-1>=0&&!state[p-1])
		dfs(d+1,p-1);
	if((p+1)%4!=0 && p+1<=11&&!state[p+1])
		dfs(d+1,p+1);
	if(p+4<=11 && !state[p+4])
		dfs(d+1,p+4);
	state[p] = false;
}
int main()
{
	for(int i =0;i<12;++i)
		state[i] = false;
	for(int i=0; i<=11; ++i)
	{	
		dfs(0,i);
	}
	cout<<my_set.size()<<endl;
	return 0;
} 

输出82，❌错误

正确代码：

#include<iostream>
#include<algorithm>
using namespace std;
int a[] = {0,0,0,0,0,0,0,1,1,1,1,1};
int s[3][4];
int num =0;
int temp_num = 0;
void dfs(int i, int j)
{
	temp_num++;
	s[i][j] = 0;
	if(temp_num == 5)
		{
			num++;
			return;
		}
	if(i-1>=0 && s[i-1][j] == 1)
		dfs(i-1,j);
	if(i+1<=2 && s[i+1][j] ==1)
		dfs(i+1,j);
	if(j+1<=3 && s[i][j+1] ==1)
		dfs(i,j+1);
	if(j-1>=0 && s[i][j-1] ==1)
		dfs(i,j-1);
}

int main()
{
	
	do{
	int px;
	int py;
	for(int i=0;i<3;++i)
		for(int j =0 ;j<4; ++j)
			if(a[i*4+j]==1)
			{
				px = i;
				py = j;
				s[i][j] = 1;
			}
			else s[i][j] = 0;
	dfs(px,py);
	temp_num = 0;		
	}while(next_permutation(a,a+12));
	
	cout<<num;	
	
}

输出116，✔正确

这个算法的思路就是枚举，当然这里面也用到了DFS，但是含义完全不同

我们总体的思想就是从这12个方格中枚举出所有的可能，然后对每种可能进行判断。

首先我们就是从12个数中随机挑选5个数，这里可以用全排列函数，通过 int a[] = {0,0,0,0,0,0,0,1,1,1,1,1};，对a数组进行全排列，通过下标映射到二维数组上，就相当于从中选择了5个数。

然后对二维数组中的这5个数，从任一点出发，进行DFS，判断搜到的个数是否为5，如果为5说明是一次剪取方法，num++。

直至对所有的组合都判断完毕。