【2019牛客暑期多校训练营 第五场 E题】【independent set 1】【状压DP】

题目链接：
https://ac.nowcoder.com/acm/contest/885/E
题意：
给一个n个点m条边的无向图，求所有子图（包括本身）的最大独立集元素个数之和。
题解:
要写这题需要了解一些位运算的知识还有最大独立集的概念，可以先去学了再来写。

定义：
此处点与点之间的关系用二进制位进行压缩，对于点$i$，用$c[i]$进行表示
如果点$i$与点$j$有边相连，则$c[i]$二进制下第$j$位为1，同理$c[j]$二进制下第$i$位为1，若无边相连则为0
而这里的点集包含什么元素也可以用一个数的二进制表示，二进制$i$位为1表示点$i$在点集中，显然空集为0，所有点都包含为$(1<<n)-1$
这里设$f[i]$为选取点状态为$i$的情况下最大独立点集元素个数

接下来就以下图为例来说明状态转移方程：

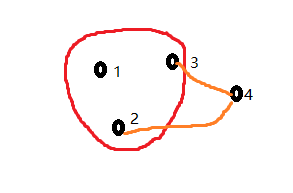
对于点集{1,2,3,4}，最大的独立点集为{1,2,3}，f[{1,2,3,4}] = 3
对于点4，如果当前最大独立点集不包含点4，则有 f[ {1,2,3,4} ] = f[ {1,2,3} ]
如果当前最大独立点集包含点4，则有 f[ {1,2,3,4} ] = f[ {1} ] + 1
不包含点4的好理解，为什么包含点4的是从f[ {1} ]转移来的呢？
这与最大独立点集的定义有关，独立点集中不包含两两相邻的点，所以与点4有关联的点全都要去掉，于是这里就去掉了点2和点3

记当前状态为x
lb_x为x二进制下第一个1位置，也就是当前点集的第一个点
那么这里状态转移方程就来了
f[x] = max(f[x ^ (1<<lb_x)], f[(x ^ num) & (~c[lb_x])] + 1)
也就是上面解释的意思，不懂的话可以对上图手动模拟一下

最后需要注意的是，这里空间只有100MB，如果开int存f[i]是会爆空间的，所以用char存

接下来上代码

代码:

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define sz sizeof
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> Pair;
const int MAX = 26;
 
int n, m;
int c[26];
char f[1 << MAX], p[1 << MAX];
 
int main() {
    ios::sync_with_stdio(0);
    cin >> n >> m;
    while (m--) {
        int u, v;
        cin >> u >> v;
        c[u] |= 1 << v;//建立关系
        c[v] |= 1 << u;
    }
    for (int i = 0; i < n; i++)p[1 << i] = i;//预处理了下lowbit(x)对应第几个点
    int ans = 0;
    f[0] = 0;
    for (int x = 0; x < (1 << n); x++) {
        int num = x & (-x), lb_x = p[num];
        f[x] = max((int)f[x ^ num], f[(x ^ num) & (~c[lb_x])] + 1);
        ans += f[x];
    }
    cout << ans << endl;
    return 0;
}