站神的 A+B problem
题意
对于0≤x≤a,0≤y≤b,0≤z≤c0 \leq x \leq a, 0 \leq y \leq b, 0 \leq z \leq c0≤x≤a,0≤y≤b,0≤z≤c
请问有多少种满足条件的三元组(x,y,z)(x, y, z)(x,y,z),满足x+y=zx + y = zx+y=z
a,b,c≤106a,b,c \leq 10 ^ 6a,b,c≤106
题解
好家伙,真正的签到题都在最后
其实这题看最开始的通过率就知道,它不是最简单的题
这时候应该转换策略,去读其他题
我看许多人提交的代码都是直接三个for暴力枚举
显然是不行的,这样复杂度是O(n3)O(n^3)O(n3)
现在来看看正解
我们不能枚举x,y,zx,y,zx,y,z三个参数,只需要枚举其中一个参数就能算出所有答案
这里为了方便,我们枚举z=1,2,3,...,cz=1,2,3,...,cz=1,2,3,...,c
当我们确定zzz的值时
xxx的范围也确定了,为[0,min(z,a)][0, min(z, a)][0,min(z,a)],不妨记为[0,k1][0, k1][0,k1],同理
yyy的范围就确定了,为[0,min(z,b)][0, min(z, b)][0,min(z,b)],不妨记为[0,k2][0, k2][0,k2]
x+y=zx+y=zx+y=z,333个参数只要确定222个,剩下的参数就固定了
即确定x=0,1,2,...,k1x=0, 1, 2, ...,k1x=0,1,2,...,k1,那么y=z−xy=z-xy=z−x也就随之确定
但是注意到xxx取到某些值时,y=z−x∉[0,k2]y=z-x \not∈[0, k2]y=z−x∈[0,k2]
所以yyy的范围还要缩小一些, 只有xxx取太大,让z−x≤0z-x\leq0z−x≤0才会有这样的情况发生
所以yyy的最终范围是[max(0,z−a),min(z,b)][max(0, z - a), min(z, b)][max(0,z−a),min(z,b)]
这样我们只需要O(n)O(n)O(n)即可计算全部答案
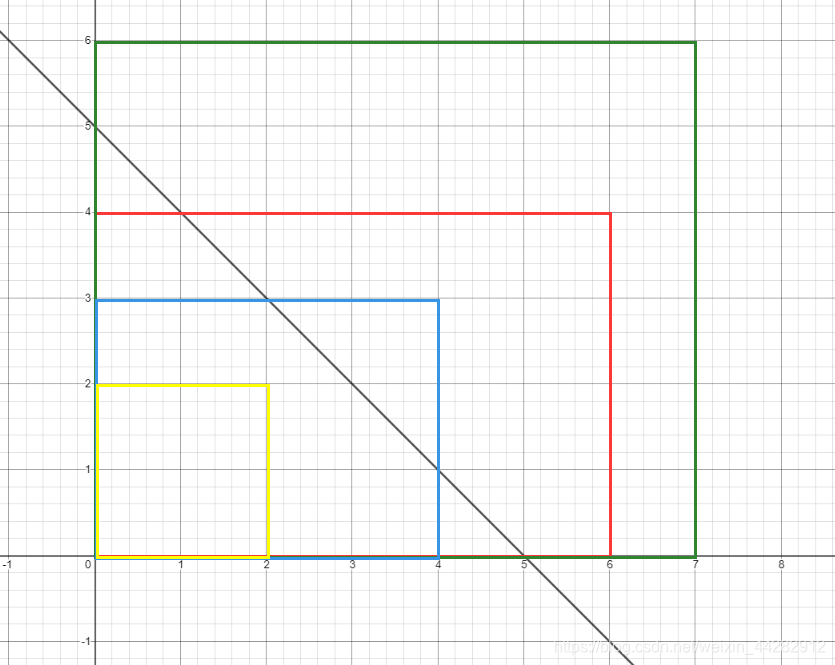
直观点当我们确定zzz的值时
相当于在二维平面上画一条直线x+y=zx+y=zx+y=z,计算落在x=[0,a],y=[0,b]x=[0,a],y =[0,b]x=[0,a],y=[0,b]上的点数
只有以下四种情况,分类讨论计算也行
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
int main() {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
long long ans = 0, mn = min(a + b, c);
//注意z最多取到min(a+b, c), 否则会出现上面黄色情况, 即所有线都在范围外面
for (int z = 0; z <= mn; z++)
ans = ans + (min(z, b) - max(0, z - a) + 1);//确定的y的范围中
printf("%lld\n", ans);
return 0;
}
站神的演讲
题意
给你一个长度为nnn的数列,求某区间的最大平均值
n≤104n\leq10^4n≤104
题解
算是一个思维题(想到了就很简单)
因为对于最大数来说,和别的数一起算平均数永远会被"平均",也就是只会变小不会变大
那么我们直接输出最大值即可
其实你们看看样例猜一猜,因为都是输出数列中最大数
代码
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
int main() {
int n;
while (scanf("%d", &n) != EOF) {
int mx = -INF;
for (int i = 1; i <= n; i++) {
int x; scanf("%d", &x);
mx = max(mx, x);
}
printf("%d\n", mx);
}
return 0;
}
打破复读机
题意
判断字符串存不存在连续两个相同字母
题解
真·签到
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
char s[N];
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%s", s + 1);
int n = strlen(s + 1), flag = 0;
for (int i = 2; i <= n; i++)
if (s[i] == s[i - 1]) flag = 1;
printf("%s\n", flag ? "Yes" : "No");
}
return 0;
}




 博客包含三道算法题,分别是站神的 A+B problem、站神的演讲和打破复读机。站神的 A+B problem 需计算满足条件的三元组数量,题解通过枚举一个参数降低复杂度;站神的演讲求数列某区间最大平均值,题解是直接输出最大值;打破复读机判断字符串有无连续相同字母。
博客包含三道算法题,分别是站神的 A+B problem、站神的演讲和打破复读机。站神的 A+B problem 需计算满足条件的三元组数量,题解通过枚举一个参数降低复杂度;站神的演讲求数列某区间最大平均值,题解是直接输出最大值;打破复读机判断字符串有无连续相同字母。
















 807
807

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








