这次一定要弄懂-SVM-1- Hard Margin SVM的原问题推导

不信邪，决定挑战下自己的能力，努力弄懂SVM
因为SVM的内容太多，求解较为复杂，分为几个部分来写，分步来搞定

第一个部分主要是介绍SVM的算法核心思想，再根据最简单的线性可分的数据集推导出原问题。
以下内容都是自己一个一个字码出来，图都是自己徒手画出来的，请尊重劳动成果。

1-1 SVM的简介

SVM（Support vector machine）中文名为支撑向量机，可以用于解决分类问题，也可以解决回归问题，采用核技术可以解决非线性问题，适用于小样本和高维特征。

核心思想在于最大化分类间隔，以提升分类器的泛化性能。

解决线性可分的SVM叫做Hard Margin SVM
解决非线性可分的SVM叫做Soft Margin SVM

对于SVM的具体算法的推导从解决最简单的问题开始：对线性可分的数据集进行分类，即推导Hard Margin SVM

1-2 线性分类器

对于线性可分的数据集，比如

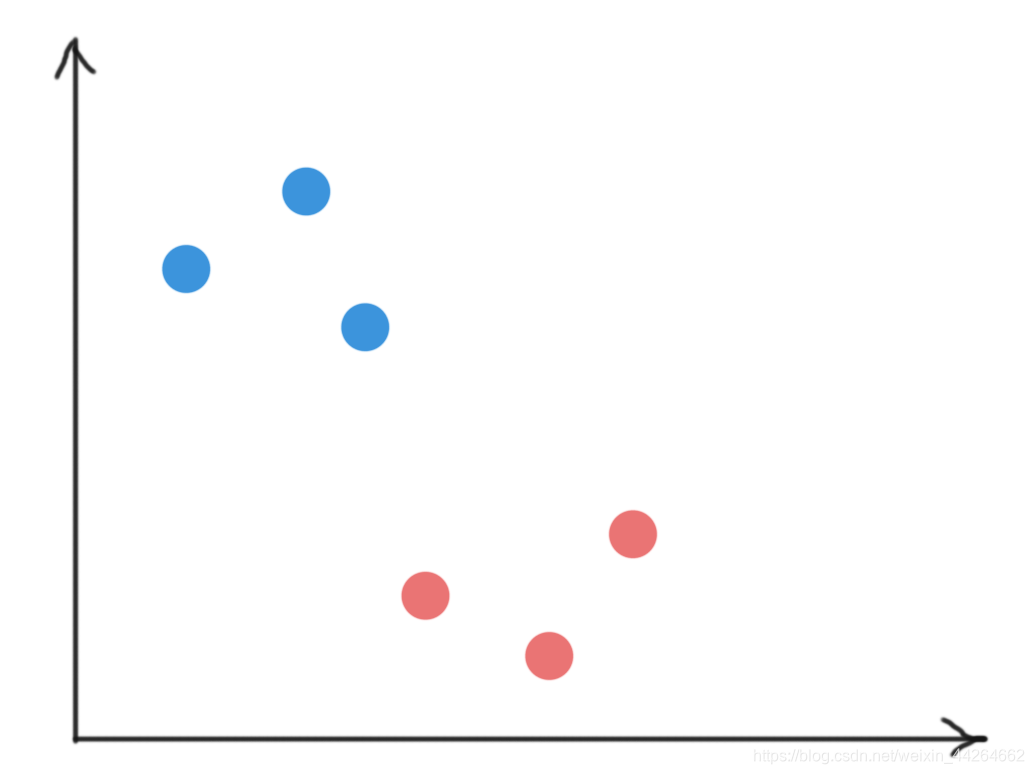
比如这样一个样本数据是线性可分的，同时，用于分割样本的直线有无数条，所以这样的问题由称之为不适定问题。

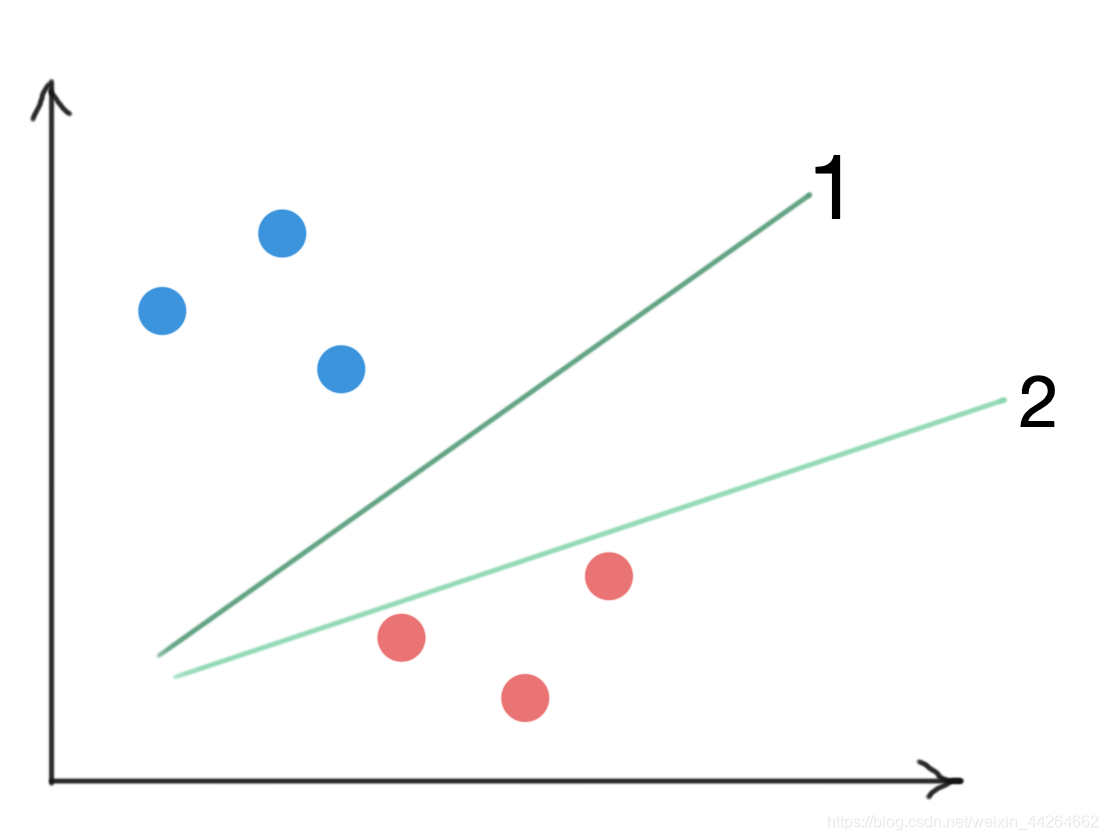
但是不同的决策边界对应的泛化能力是不同的，明显我们会认为，直线1比直线2，在分类时的泛化能力更好。
这是因为，直线1不仅对所有的样本进行了分类，而且离两个类的样本尽可能的远。这就是SVM的核心思想，。

1-3 SVM中的名词解释

支撑向量

SVM的核心思想是最大化分离间隔，关键是远离那些靠近决策边界的点。
那些距离决策边界最近的样本，称为支撑向量。

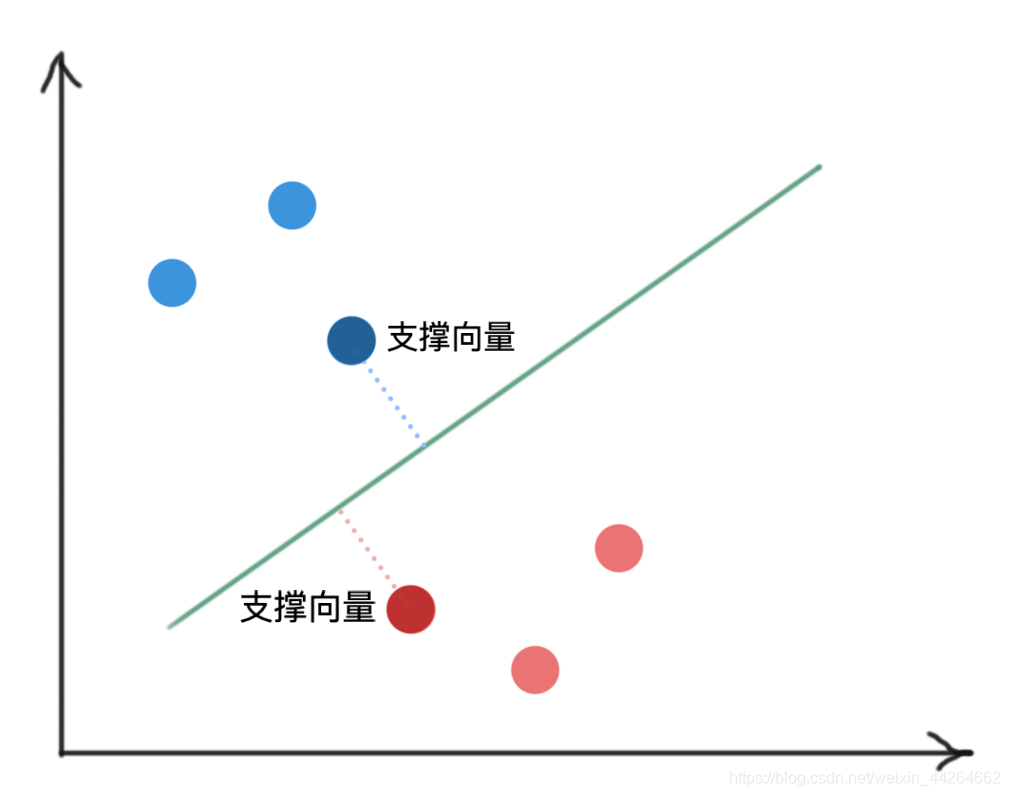
图中被加深的两个向量就是支撑向量，也就是距离决策边界最近的向量

分类间隔(margin)

支撑向量定义了一个边界区域，这个边界区域的距离叫做分类间隔(margin)，我们要找的决策边界就是位于这个区域中间的那根线。

通过示意图可以看出，决策边界到支撑向量之间的距离$d=\frac{1}{2}margin$

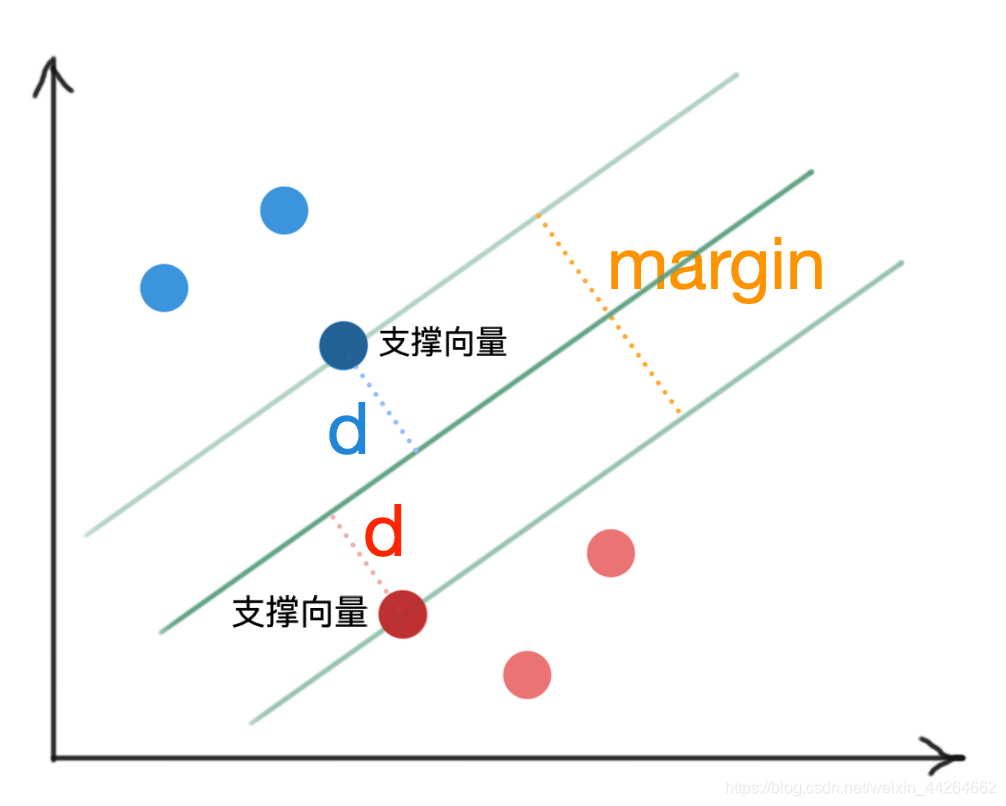
SVM要做的就是最大化d（即支撑向量到决策边界的距离），其实也是最大化margin，所以在吴恩达老师的机器学习课程中也将SVM称之为最大间隔分类器。

1-4 Hard Margin SVM 原问题推导

根据上面的过程，我们已经知道，要找的分类边界的要满足2个要求：
要求1:分类边界要保证样本正确分类
要求2:分类边界是距离支撑向量最远的直线，也就是margin或者d最大的直线

理解好两个要求的几何含义后，我们接下来要做的就是将几何含义翻译成数学表达，写出SVM要求解的原问题。

先讲解两个补充知识：

• 超平面的表达式的小细节
• 在已知决策边界的前提下，我们如何进行样本的类别预测

超平面的表达式的小细节

在线性可分的问题中，我们的决策边界是一个超平面，所以决策边界的表达式是${\omega }^T\mathbf{x}+b=0$，
其中$\omega$称为权重向量，b称为偏置项。

这个表达式存在一个小细节，也就是
如果将确定的$\omega$和b乘上一个系数k，即$k{\omega }^T\mathbf{x}+kb=0$得到的还是同一个超平面，但是表达式不同的。

举个二维平面的例子，比如直线y=x+1与直线2y=2x+2，其实指的是同一条直线。

在这里我们先了解这样一个结论：
对于超平面的表达式，$\omega$和b乘上一个系数后，得到的仍是原来的超平面。

在已知决策边界的前提下，我们如何进行样本的类别预测呢？

在SVM问题中，我们将正样本用+1表示，负样本用-1表示，只需要将$\mathbf{x}$中的特征向量带入决策边界中，如果计算结果>0，则分为正样本，如果计算结果<0，则分为负样本。

即：

$$\{\begin{array}{rcl}{\omega }^T\mathbf{x}+b\ge 0& & y=+1(正样本)\\ {\omega }^T\mathbf{x}+b<0& & y=-1(负样本)\end{array}$$

要求2:让margin或者d最大

我们先将要求2翻译成数学语言。
既然要d最大，那我们就需要表示d的大小。

d是支撑向量到决策边界的距离，即点到直线的距离。
补充下点到直线的距离公式，以三维空间为例，
点(x0,y0,z0)到直线Ax+By+Cz+d=0的距离为:
$$d=\frac{|A{x}_0+B{y}_0+C{z}_0+d|}{\sqrt{A^2+B^2+C^2}}$$

这里{A,B,C}对应的是权重向量$\omega$，
d对应的是偏置项

由此我们可以推出更一般的情形下的距离表达：
分子是将点的坐标带入直线中的绝对值
分母是权重向量的膜

所以我们要求的d表示为:
$$d=\frac{|{\omega }^{\mathbf{T}}{\mathbf{x}}_{支撑向量}+b|}{||w||}$$
其中x为支撑向量的值

我们要做的就是max⁡ω,bd\max \limits_{\bold{\omega},b}d