JS递归思想&递归函数执行顺序

递归思想类似与数学中的归纳法，即需要完成一个复杂函数的运算的时候，先算出他的上一步的结果然后继续运算。

复杂情况的递归建议转化为树的结构进行思考。

递归函数包括的内容：

1.函数的结束条件；

2.过程处理逻辑；

3.下一个递归函数的进行；

//leetcode22:括号的生成，递归回溯解题，index用来记录函数执行的过程    
用index记录函数的执行过程
    var index = 0;
    var generate = function(n){
        
        const res = [];
        if(n<= 0){
            console.log(res);
            return res;
        }
        const dfs = function(path,open,close){
            index++;
        //记录每次进入递归函数的输入path
           console.log("start:",path,open,close,index)
            // if(open > n || close>open){
            //     return ;
            // }
            if(path.length == 2*n){
                res.push(path);
                return;
            }
            dfs(path+'(',open +1 ,close);
        //验证什么时候开始执行递归函数的下一层逻辑
            console.log('index afetr open:',index + path)
            dfs(path+')',open , close+1);
        //验证什么时候开始执行到递归函数的最后；
            console.log("end:",path,open,close)
        }
        dfs("",0,0);
        console.log('res:',res);
        return res;
    }

通过打印日志，整理递归函数的执行逻辑。

本次函数的功能相当于对完全二叉树的遍历，n=1，即完全二叉树共有7个节点，函数一共执行7次。

 函数执行到open+1处，如果没有遇到return条件，将一直递归下去，且不会继续执行该语句下面的函数，直到return；

弹出return的上一个参数条件，继续执行函数的下一个语句，同理，直到return；

函数执行过程

次序	path	open	close	index
①	‘ ’	0	0	1
②	（	1	0	2：不满足return条件，继续递归
③	（（	2	0	3：满足条件return，返回到上一个递归函数的执行过程中②，继续往下走，即递归函数的参数变为②中的参数
④	（）	1	1	4：③return后，返回到②，继续向下走，进入close+1的递归，满足条件，return到进入④的过程，即②；return到②后，函数中无再次调用递归，所以虽无return 但正常end②过程，return到open递归的①，向下执行；
⑤	）	0	1	5：open的递归函数，return到①后，path为空，继续向下执行，进入到close的递归函数，
⑥	)(	1	1	6:⑤执行时，首先遇到open+1的递归即⑥，满足return条件，open的递归return到⑤，继续向下执行，
⑦	））	0	2	7：⑥return到⑤后，继续向下执行进入close的递归⑦，满足return条件，return到进入⑥的过程⑤，无再递归函数的调用，end过程⑤，⑤由①进入，end⑤以后，return到①，执行①的最后一句，结束递归。

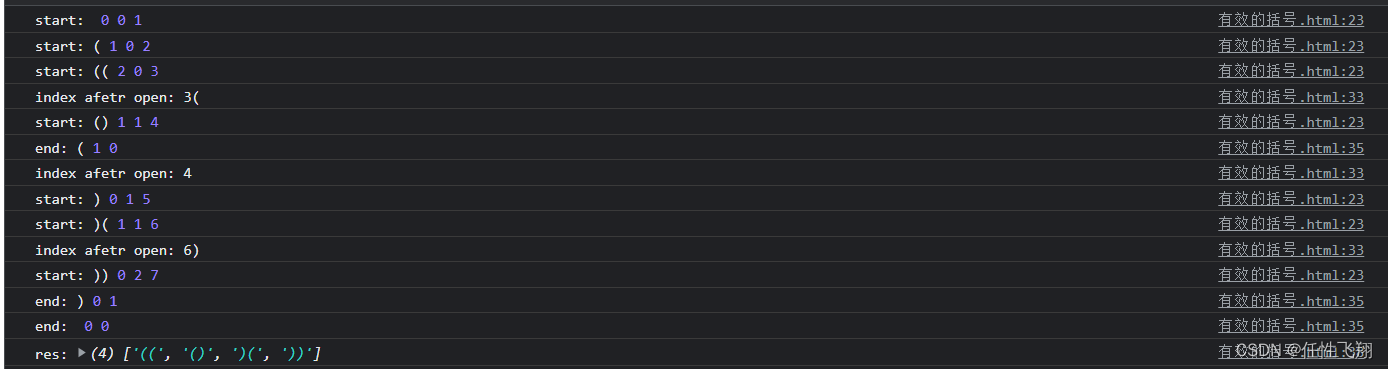
 总结：递归的总过程，可以理解为入栈和出栈；

入栈：执行递归语句之前的函数，一般为判断是否return，有时候可以对参数进行处理，方便结果的整理  或者再次递归；

出栈：执行递归语句之后的函数，即可以对刚出栈的结果进行二次加工后再次入栈，或者返回