BCH_RS编码

一、内容

1、BCH码编码
2、BCH码译码
3、RS码编码
4、RS码译码
5、手动测试
6、自动测试

二、功能模块

实现了码长可变、纠错能力可变、BSC信道、BCH译码用快速迭代译码、钱搜索算法寻找错误位置、RS译码用迭代译码、钱搜索算法、福尼算法实现。
1、构造多项式到向量及向量到多项式的对照表
2、生成极小多项式
3、求多项式的次数模块
4、多项式加法
5、向量乘法
6、多项式乘法
7、求BCH码生成多项式
8、求RS码生成多项式
9、BCH码、RS码编码
10、求f(x)，代表已知多项式求f(x),x为向量
11、BCH迭代译码、钱搜索算法
12、RS迭代译码、钱搜索算法、福尼算法
13、手动测试
14、自动测试
15、BSC信道

三、结果展示

1 手动测试

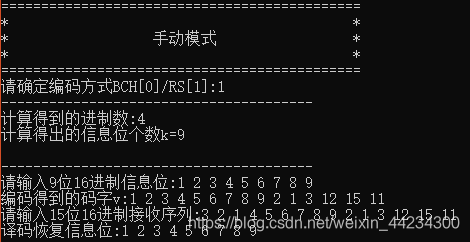
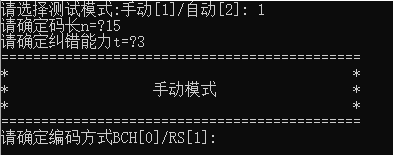
2 自动测试

四、C++实现

本实验是基于Dev C++环境进行的。由于功能模块的数量太多，在实验报告中展示会显得杂乱繁琐，故只在实验报告中简述C语言编程的实现思想，详见提交的实验源码。
用一个int数组来存储本原多项式表，每个本原多项式用int型数表示；用一个int数组表示多项式，如果是BCH里面存储的是0或1，RS码存储的是多进制数的向量形式；生成两个表格分别为向量到方幂以及方幂到向量表；迭代译码的过程中每一步的结果用一个结构体来存储，所有的迭代步骤就构成了一个结构体数组。BSC信道是用一个与编码发送比特流相同的数组实现的，错误设为1，不错设为0，再与发送比特流进行异或运算得到接收比特流。
1、求极小多项式模块
使用共轭根系法求极小多项式，得到一个数组为对每一个GF（2m）的向量存存储着其共轭根系。
2、多项式乘法模块，输入两个表示多项式的数组，输出相乘后的数组，相乘时每个向量依次相乘在根据次数移位。
3、BCH码生成多项式模块，由输入的t确定出一组向量，在找到每个向量的共轭根系，求各个共轭根系的并集，在依次乘以一次多项式得到生成多项式。
4、编码模块，信息多项式同样用一个数组表示作为输入，生成多项式数组也作为输入，根据v(x)=〖x^r m(x) +(x^r m(x))〗_g(x) 得到编码后的多项式数组。具体就是移位和进行异或运算。
5、译码模块，用迭代译码算法，RS和BCH的译码分别写了一个模块，迭代译码的过程中每一步的结果用一个结构体来存储，所有的迭代步骤就构成了一个结构体数组，同时为了提高效率加入了快速译码、钱搜索算法和福尼算法。
6、BSC信道，BSC信道是用一个与编码发送比特流相同的数组实现的，错误设为1，不错设为0，其中1以信道转移概率出现，再与发送比特流进行异或运算得到接收比特流。

五、结果分析

1 对比相同码长不同纠错能力时的误码率。

可以看出，当相同码长时纠错能力增大，误码率减小，原因是冗余位增加，但码率减小。

2、对比相同纠错能力不同码长的误码率

可以看出，相同纠错能力下，码长越长冗余位越多，误码率越小。

3、对比RS码和BCH码的误码率

由于RS码是纠突发错误的纠错码，BCH码纠随机错误，而BSC信道是随错误信道，故RS码的误码率比BCH码高。

六、完整代码

# include<stdio.h>
# include<vector>
# include<iostream>
# include<cmath>
# include<set> 
# include<numeric>
# include<string>
# include<string.h>
# include<algorithm>
# include<stdlib.h> 
# include<time.h>
# include<fstream>
using namespace std;
const int N=10000;//设计的最长码长 
struct die{
   //迭代过程表 
		int u;
		int deta[N];
		int D;
		int u_d;//u-D
		int du;
	};

vector<int> a_v,v_a;
	
void excel(int n, vector<int> &a_v, vector<int> &v_a){
   
	//int n;//码长
	//vector<int> a_v;//多项式到向量
	//vector<int> v_a;//向量到多项式 
	int m=int(log(double(n+1))/log(2.0));
	int benyuan[26]={
   0};
	//============本原多项式表===============// 
	benyuan[ 2]=1 + (1<<1) + (1<<2);
	benyuan[ 3]=1 + (1<<1) + (1<<3);
	benyuan[ 4]=1 + (1<<1) + (1<<4);
	benyuan[ 5]=1 + (1<<2) + (1<<5);
	benyuan[ 6]=1 + (1<<1) + (1<<6);
	benyuan[ 7]=1 + (1<<3) + (1<<7);
	benyuan[ 8]=1 + (1<<2) + (1<<3) + (1<<4) + (1<<8);
	benyuan[ 9]=1 + (1<<4) + (1<<9);
	benyuan[10]=1 + (1<<3) + (1<<10);
	benyuan[11]=1 + (1<<2) + (1<<11);
	benyuan[12]=1 + (1<<1) + (1<<4) + (1<<4) + (1<<6) + (1<<12);
	benyuan[13]=1 + (1<<1) + (1<<3) + (1<<4) + (1<<13);
	benyuan[14]=1 + (1<<1) + (1<<6) + (1<<10) + (1<<14);
	benyuan[15]=1 + (1<<1) + (1<<15);
	benyuan[16]=1 + (1<<1) + (1<<3) + (1<<12) + (1<<16);
	benyuan[17]=1 + (1<<3) + (1<<17);
	benyuan[18]=1 + (1<<7) + (1<<18);
	benyuan[19]=1 + (1<<1) + (1<<2) + (1<<5) + (1<<19);
	benyuan[20]=1 + (1<<3) + (1<<20);
	benyuan[21]=1 + (1<<2) + (1<<21);
	benyuan[22]=1 + (1<<1) + (1<<22);
	benyuan[23]=1 + (1<<5) + (1<<23);
	benyuan[24]=1 + (1<<1) + (1<<2) + (1<<7) + (1<<24);
	benyuan[25]=1 + (1<<3) + (1<<25);
	//=============打表================// 
	int f=benyuan[m];//本原多项式 
	for(int i=0;i<(1<<m);i++) v_a.push_back(-1); 
	int v=1;
	for(int i=0;i<(1<<m)-1;i++){
   
		a_v.push_back(v);
		v_a[v]=i;
		v=v<<1;
		if(v>=(1<<m)) v=v^f;
	}
}


void min_a(int n,vector<vector<int> > &mina){
   
	//==================极小多项式================// 
	//码长 n=2^m-1
	//vector<vector<int> > mina,极小多项式
	vector<int> temp;
	temp.push_back(0);
	for(int i=0;i<n;i++)  mina.push_back(temp);
	bool hash[1<<20]={
   false};
	int first_no=0;//是否迭代完 
	while(first_no<n){
   
		temp.clear();
		temp.push_back(first_no);
		for(int i=1;;i++){
   
			if((first_no*(1<<i))%n==first_no) break;
			temp.push_back((first_no*(1<<i))%n);
		}
		for(int i=0;i<temp.size();i++){
   
			mina[temp[i]]=temp;
			hash[temp[i]]=true;
		}
		for(int i=0;;i++){
   
			if(!hash[i]){
   
				first_no=i;
				break;
			}
		}
		
	} 
}


int alpha(int* g){
   
	//===============求多项式g的次数===========
	int sum=accumulate(g,g+N,0);
	int n=0;
	int temp;
	while(true){
   
		temp=accumulate(g,g+n+1,0);
		if(temp==sum) break;
		n++;
	}
	return n;
}

int max_two(int a,int b){
   
	//===============求两数最大值================ 
	if(a>b) return a;
	else return b;
}

void sum(int* a,int* b,int* out){
   
	//================码多项式加法=================== 
	//a,b输入码字,存储向量表示 
	//out 输出码字
	fill(out,out+N,0);
	for(int i=0;i<=max_two(alpha(a),alpha(b));i++){
   
		out[i]=a[i]^b[i];
	}
}

int amul(int a,int b,int n){
   
	//=========