pso粒子群优化算法+MATLAB代码

pso粒子群优化算法

1.概念

粒子群算法最早是由Eberhart和Kennedy于1995年提出的，属于进化算法的一种，它的基本概念源于对鸟群觅食行为的研究。用一种粒子来模拟鸟类个体，每个粒子可视为多维搜索空间中的一个搜索个体，粒子的当前位置即为对应优化问题的一个候选解，粒子的飞行过程即为该个体的搜索过程，粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整，粒子仅具有速度和位置两种属性，速度代表移动的快慢，位置代表移动的方向，每个粒子单独搜寻的最优解叫做个体极值，粒子群中最优的个体极值作为当前全局最优解，通过在迭代过程中更新种群速度和位置，最终得到满足终止条件的最优解。

2.算法思想

简介

基础公式：

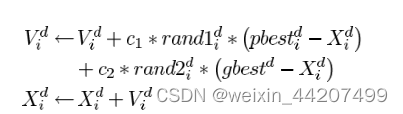
• 假设在一个D维的目标搜索空间中，有N个粒子组成的一个群体，其中第i个粒子的位置表示为一个D维向量：

$$X_i=(x_{i1},x_{i2},...x_{iD}),i=1,2,3,...,N$$

• 第i个粒子的“飞行”速度也是一个D维向量，记为：

$$V_i=(v_{i1},v_{i2},...v_{iD}),i=1,2,3,...,N$$

• 第t代的第i个粒子向t+1代进化时，根据以下式子更新（带惯性权重的pso）：

$$v_{ij}(t+1)=w{v}_{ij}(t)+c_1\ast ran{d}_1(t)[pbes{t}_{ij}(t)-x_{ij}(t)]+c_2\ast ran{d}_2(t)[gbes{t}_{gj}(t)-x_{ij}(t)]$$

$$x_{ij}(t+1)=x_{ij}(t)+v_{ij}(t+1)$$

• 其中：

1. ​ rand1和rand2为[0,1]的随机数，用于控制个体最优方向和群体左右方向在移动过程中的权值比重。

2. ​ pbest为个体历史经过的最优位置，gbest为全体历史最优位置。根据新位置的适应度来判断是否要更新pbest或gbest。

   ​ 该算法一般用于求函数极值，所以一般取该位置函数的值为适应度，

3. ​ c1,c2为调节pbest和gbest相对重要性的加速因子，c1为个体学习系数，c2为全体学习系数均取定值 1.49445

4. ​ w为惯性权重，为保留原来方向的速度。（最好前期大一些，保证搜索范围；后期小一些，便于向其他粒子学习，不会飞过）

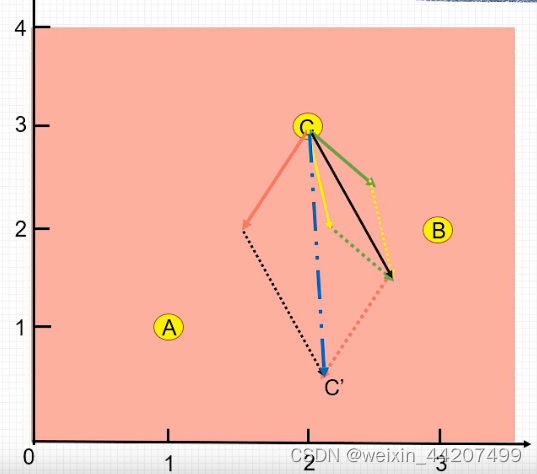
示例：

C为粒子当前位置，A为全局最优位置，对应gbest，B为自身最优，对应pbest。

$$v_{ij}(t+1)=w{v}_{ij}(t)+c_1\ast ran{d}_1(t)[pbes{t}_{ij}(t)-x_{ij}(t)]+c_2\ast ran{d}_2(t)[gbes{t}_{gj}(t)-x_{ij}(t)]$$

黄色线为C当前飞行方向，绿色为个体最优步长，红色为全局最优步长。蓝色为下一步要飞行的方向和距离。

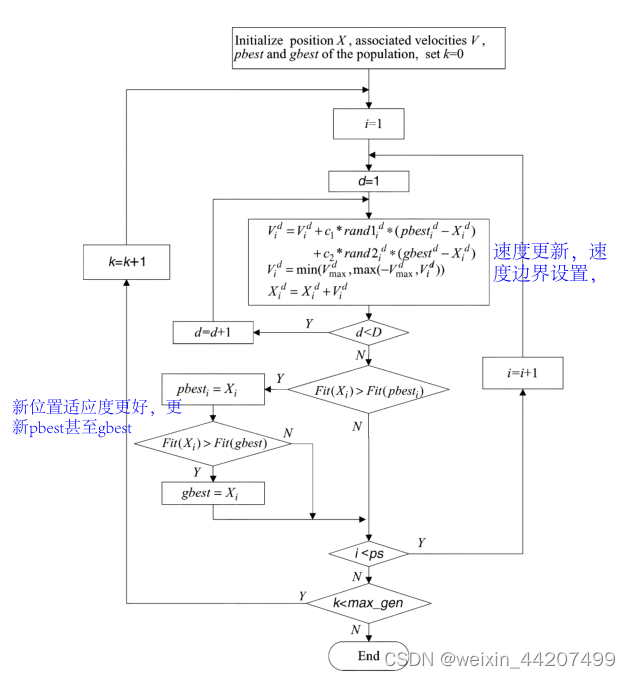
3.算法流程

$$输入参数：w（可为线性函数递减）,c_1,c_2:0.1-2(一般取1.49455)，v_{max},x_{max}:取决于优化函数$$

1.初始化种群x

2.计算个体适应度*

3.更新粒子速度—>更新粒子位置

4.计算新位置的适应度，若新位置的适应度更高，则更新粒子pbest并判断更新gbest，否则不更新？。

5.判断终止条件(设定迭代进化次数，适应度n代不再变化等)

• 一般的，优化目标是最小化函数值。所以个体计算出的函数值越小，适应度越高

• max f=min -f

• 更新速度后，先进行速度边界检测，一般采用$$v>v_{max}=v_{max},同理，x>x_{max}=x_{max}$$

  pso 流程图：

演示图：

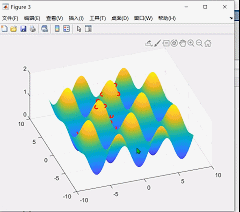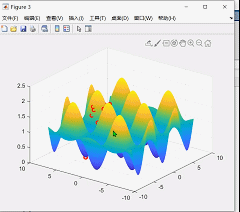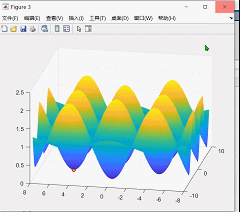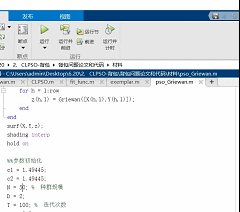
4.算法不足

受pbest和gbest的影响，求解多峰问题时早熟收敛，容易陷入局部最优解。

• 当前gbest并非实际最优解，但是粒子可能会受他影响偏离实际最优解的位置 ，飞向局部最优
• pbest和gbest的位置过于接近，导致粒子过早陷入局部最优

$$v_{ij}(t+1)=w{v}_{ij}(t)+c_1\ast ran{d}_1(t)[pbes{t}_{ij}(t)-x_{ij}(t)]+c_2\ast ran{d}_2(t)[gbes{t}_{gj}(t)-x_{ij}(t)]$$

5.算法优化

1.实现参数自适应变化，如w

2.引入一些其他机制，如随机因素，速度、位置边界变化，压缩后期最大速度等

3.结合其他只能优化算法，遗传算法，模拟退火算法，帮助跳出局部最优

6.代码

%%清空环境
clc;
clear;
%格里旺克函数
%%绘制目标函数曲线
figure
x = -8:0.1:8;
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1:col
	for h = 1:row
        z(h,l) = Griewan([X(h,l),Y(h,l)]);
	end
end
surf(X,Y,z);
shading interp
hold on

%%参数初始化
c1 = 1.49445;
c2 = 1.49445;
N = 50; %　种群规模
D = 2;
T = 100; %　迭代次数
wa = 0.9;
wi = 0.4;
Xmax = 8 ;
Xmin = -8 ;
Vmax = 1 ; %　最大飞行速度
Vmin = -1 ; %　最小飞行速度

% Xm(i,:)粒子i位置

%%产生初始粒子和速度
for i=1:N
    Xm(i,:)=8*rands(1,2);    %初始位置  N*2的矩阵，第i行表示第i个粒子的位置
    V(i,:)=rands(1,2);       %初始速度 
    fitness(i)=Griewan(Xm(i,:));  %粒子初始适应度，即函数值
    
     xm=Xm(i,:);            % xm为初始位置
     f(i,:)=fitness(i);   % f i   为粒子i初始适应度  
     %scatter3( xm(:,1),xm(:,2) ,fitness(i),'r*' );  %打印粒子初始位置
     %plot(xm,'ro')  
end

%%个体极值与群体极值
[bestfitness,bestindex]=min(fitness);   %bestfitness=最佳适应度，bestindex为最佳适应度的粒子，为第几个
pbest = Xm;               %个体最优初始为他本身位置  pbest存所有粒子的个人最优位置           
gbest = Xm(bestindex,:);  %全局最优为找出来的最佳适应值的那个粒子，第bestindex个粒子的位置
fitnesspbest=fitness;     %个体历史最佳适应度为初始值
fitnessgbest=bestfitness; %全局历史最佳最佳适应度为找出来的最佳度



%%迭代寻优
for i=1:T    %从第一代到第T代，当前代数为i
    w=wa-(wa-wi)*i/T;     %wa=0.9 wi=0.4 w=0.9-0.5*(i/T)   w(0.9-0.4)前期w大，适合保持自己速度充分寻找，后期w小便于向其他学习
    for j=1:N  %N个粒子，当前为第j个
        %速度更新
        V(j,:)=w*V(j,:)+c1*rand*(pbest(j,:)-Xm(j,:))+c2*rand*(gbest-Xm(j,:));  %速度矩阵第j行更新
        V(j,find(V(j,:)>Vmax))=Vmax; 
        V(j,find(V(j,:)<Vmin))=Vmin;
        %种群更新
        Xm(j,:)=Xm(j,:)+V(j,:);                      %位置矩阵第j行更新
        Xm(j,find(Xm(j,:)>Xmax))=Xmax;
        Xm(j,find(Xm(j,:)<Xmin))=Xmin;
        %适应度值更新
        fitness(j)=Griewan(Xm(j,:));                %第j个粒子的适应度更新
        
    end
     dt=plot3(Xm(:,1),Xm(:,2),fitness(:),'bo','linewidth',2)    % 动态绘图
     pause(0.1)  
     delete(dt)

    
    for j=1:N
        %个体最优更新
        if fitness(j)<fitnesspbest(j)   %第j个粒子更新后适应度
            pbest(j,:)=Xm(j,:);
            fitnesspbest(j)=fitness(j);
     
        end
        
        if fitness(j)<fitnessgbest
            gbest=Xm(j,:);
            fitnessgbest=fitness(j);
        end    
    end
    
   
     
    yy(i)=fitnessgbest;
end  

%%输出结果
fitnessgbest=fitnessgbest
Xgbest=gbest

plot3(gbest(1),gbest(2),fitnessgbest,'ro','linewidth',2)   % 打印最佳粒子的位置

figure
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);
ylabel('适应度','fontsize',12);