03 位移变换Transformation
2维齐次变换矩阵

引入齐次坐标,点设为1,向量设为0

点和向量的坐标表示有一个非常重要的区别,即最后一个维度是0 or 1(如图橙色部分)。这样设计有两个目的:
-
向量具有平移不变性,给向量最后一个维度设为0,目的就是保护向量经过平移变换之后不变。
-
便于点和坐标之间的转换运算。

point + point = 两点之间的中点
使用齐次坐标还有一个好处,所有的变化(平移、旋转)都可以包含在一个矩阵中:

逆变换
即逆矩阵
复杂变换
存在多个变换矩阵时,变换顺序从右到左

3维齐次变换矩阵
与2维原理类似,只是多了一个维度

旋转矩阵

沿任意轴n旋转a°:
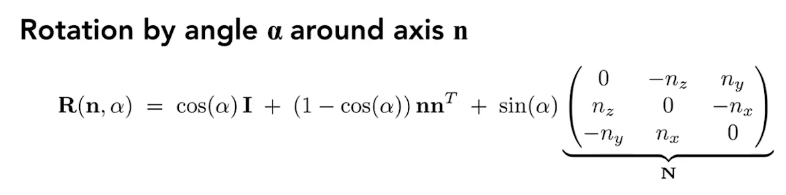
相机/视图变换

设相机坐标position为(x,y,z),相机看向的方向为g,相机正上方向量为t,变换矩阵为
M
v
i
e
w
M_{view}
Mview
M
v
i
e
w
=
R
v
i
e
w
T
v
i
e
w
T
v
i
e
w
=
(
1
0
0
−
x
e
0
1
0
−
y
e
0
0
1
−
z
e
0
0
0
1
)
R
v
i
e
w
=
(
x
g
×
t
y
g
×
t
z
g
×
t
0
x
t
y
t
z
t
0
x
−
g
y
−
g
z
−
g
0
0
0
0
1
)
M_{view}=R_{view}T_{view}\\ T_{view}=\begin{pmatrix} 1&0&0&-x_e\\ 0&1&0&-y_e\\ 0&0&1&-z_e\\ 0&0&0&1\end{pmatrix}\\ R_{view}=\begin{pmatrix} x_{g\times t}&y_{g\times t}&z_{g\times t}&0\\ x_{t}&y_{t}&z_{t}&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1\end{pmatrix}\\
Mview=RviewTviewTview=
100001000010−xe−ye−ze1
Rview=
xg×txtx−g0yg×tyty−g0zg×tztz−g00001
g to -Z, t to Y,(g×t) to X
04 透视投影和正交投影
正交投影
正交投影的做法就是把物体移到原点处的 [-1,1]^3 的标准立方体中。

步骤分为两步:
① 先将物体中心平移到原点。
②再进行缩放,缩放到[-1,1]^3 的标准立方体中。
M
o
r
t
h
o
=
(
2
r
−
l
0
0
0
0
2
t
−
b
0
0
0
0
2
n
−
f
0
0
0
0
1
)
(
1
0
0
−
r
+
l
2
0
1
0
−
t
+
b
2
0
0
1
−
n
+
f
2
0
0
0
1
)
M_{ortho}=\begin{pmatrix} \frac2{r-l}&0&0&0\\ 0&\frac2{t-b}&0&0\\ 0&0&\frac2{n-f}&0\\ 0&0&0&1\\ \end{pmatrix} \begin{pmatrix} 1&0&0&-\frac{r+l}2\\ 0&1&0&-\frac{t+b}2\\ 0&0&1&-\frac{n+f}2\\ 0&0&0&1\\ \end{pmatrix}
Mortho=
r−l20000t−b20000n−f200001
100001000010−2r+l−2t+b−2n+f1
透视投影


透视投影可分为两步:
step 1:挤压远平面,将远平面变换为与近平面一样大小
step 2:使用正交投影将远平面投影到近平面上
整个过程中,近平面上的点无变化,远平面的中心点也不变
挤压之后,内部的某个点的z会变大,更偏向于f
设透视变正交矩阵为
M
p
e
r
s
p
−
>
o
r
t
h
o
M_{persp->ortho}
Mpersp−>ortho,透视投影矩阵为
M
p
r
e
s
p
M_{presp}
Mpresp
M
p
e
r
s
p
−
>
o
r
t
h
o
=
(
n
0
0
0
0
n
0
0
0
0
n
+
f
−
n
f
0
0
1
0
)
M
p
e
r
s
p
=
M
o
r
t
h
o
M
p
e
r
s
p
−
>
o
r
t
h
o
M_{persp->ortho}=\begin{pmatrix} n&0&0&0\\ 0&n&0&0\\ 0&0&n+f&-nf\\ 0&0&1&0\end{pmatrix}\\ M_{persp}=M_{ortho}M_{persp->ortho}
Mpersp−>ortho=
n0000n0000n+f100−nf0
Mpersp=MorthoMpersp−>ortho
具体推导过程见https://www.bilibili.com/video/BV1X7411F744?p=4
根据四个参数即可得到透视投影变换矩阵,可利用fovY和aspect求出正交投影中的l, r, b ,t
- n:近平面距离
- f:远平面距离
- fovY:视锥角
- aspect:宽高比

05 光栅化
MVP矩阵
M:模型Model transfomation
V:观察View transformation
P:投影Projection transformation(Orthographic or Perspective)
M
v
i
e
w
p
o
r
t
=
(
w
i
d
t
h
2
0
0
w
i
d
t
h
2
0
h
e
i
g
h
t
2
0
h
e
i
g
h
t
2
0
0
1
0
0
0
0
1
)
M_{viewport}=\begin{pmatrix} \frac{width}2&0&0&\frac{width}2\\ 0&\frac{height}2&0&\frac{height}2\\ 0&0&1&0\\ 0&0&0&1\\ \end{pmatrix}
Mviewport=
2width00002height0000102width2height01
采样
将连续函数离散化的过程,是图形学中的重要概念

抗锯齿(反走样)

Aliasing Artifacts走样:信号变化太快导致采样速度跟不上
Artifacts:图形学中针对Errors/Mistakes/Inaccuracies的统称,可理解为图像处理中产生的瑕疵,锯齿就是采样中产生的Artifacts之一

如图,越高频的函数f1->f5,相同频率采样时走样越严重

MSAA抗锯齿
不提升采样率(分辨率),而是使用低通滤波,将高频信号去掉,剩下信号再使用采样,就可以降低走样率

使用滤波,先对对象模糊处理再进行采样(顺序不可逆)

e.g.使用一个2×2的滤波器,判断每个像素点内有多少个点(覆盖率)

根据覆盖率获得每个像素点的深浅

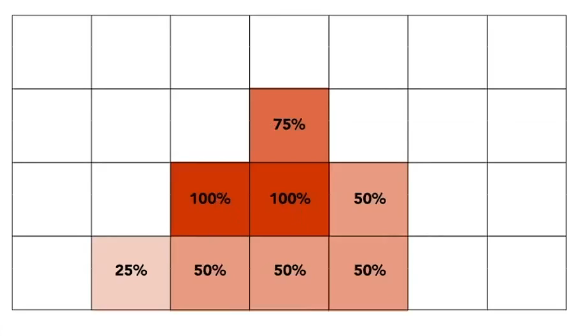
MSAA的代价:计算量增加
其他抗锯齿方案:
- FXAA(Fast Approximate AA):图像后处理
- TAA(Temporal AA):引入时间概念,复用上一帧的结果
滤波Filtering
去掉一系列频率,从时域到频域
滤波前:

滤波后:
高通滤波
去除低频,只剩下高频信息。由图可知高频信息基本就是图像边界轮廓

低通滤波
去除高频,只留低频信息

中通滤波

卷积Convolution
滤波=平均=卷积
时域的卷积对应频域的乘积,反之亦然
如图,任何一个像素都等于它周围3×3范围内像素的平均,这便是一次卷积

使用越大的卷积盒,就会让图像变得越模糊,即越低通的滤波
待更新……


























 509
509

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








