超详细递归实现汉诺塔

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。——百度百科

递归的精髓是大事化小,所以我们先从简单的开始研究.

一层汉诺塔时.

两层汉诺塔时

 三层汉诺塔时

分析可得解开汉诺塔步骤是

1.将上面的(n-1) 层塔放到中转塔(B)上.

2.将第n层塔放到目标塔(C)上.

3.将中转塔上的放到目标塔(C)上

函数实现

#include <stdio.h>
移动函数
void Move(char pos1, char pos2)
{
	printf(" %c->%c ", pos1, pos2);
}
//posA起始位置, posB中转位置, posC目标位置
void Hanoi(int n, char posA, char posB, char posC)
{
	if (1 == n)
	{
		Move(posA, posC);
	}
	else
	{
		//将除最低层的塔转移到中转塔上----步骤1
		Hanoi(n - 1, posA, posC, posB);
		//将最底层的塔放到目标塔上-----步骤2
		Move(posA, posC);
		//将除最底层的塔放到目标塔上-----步骤3
		Hanoi(n - 1, posB, posA, posC);
	}
}
int main()
{
	Hanoi(3, 'A', 'B', 'C');
	return 0;

 步骤分析

n=2时

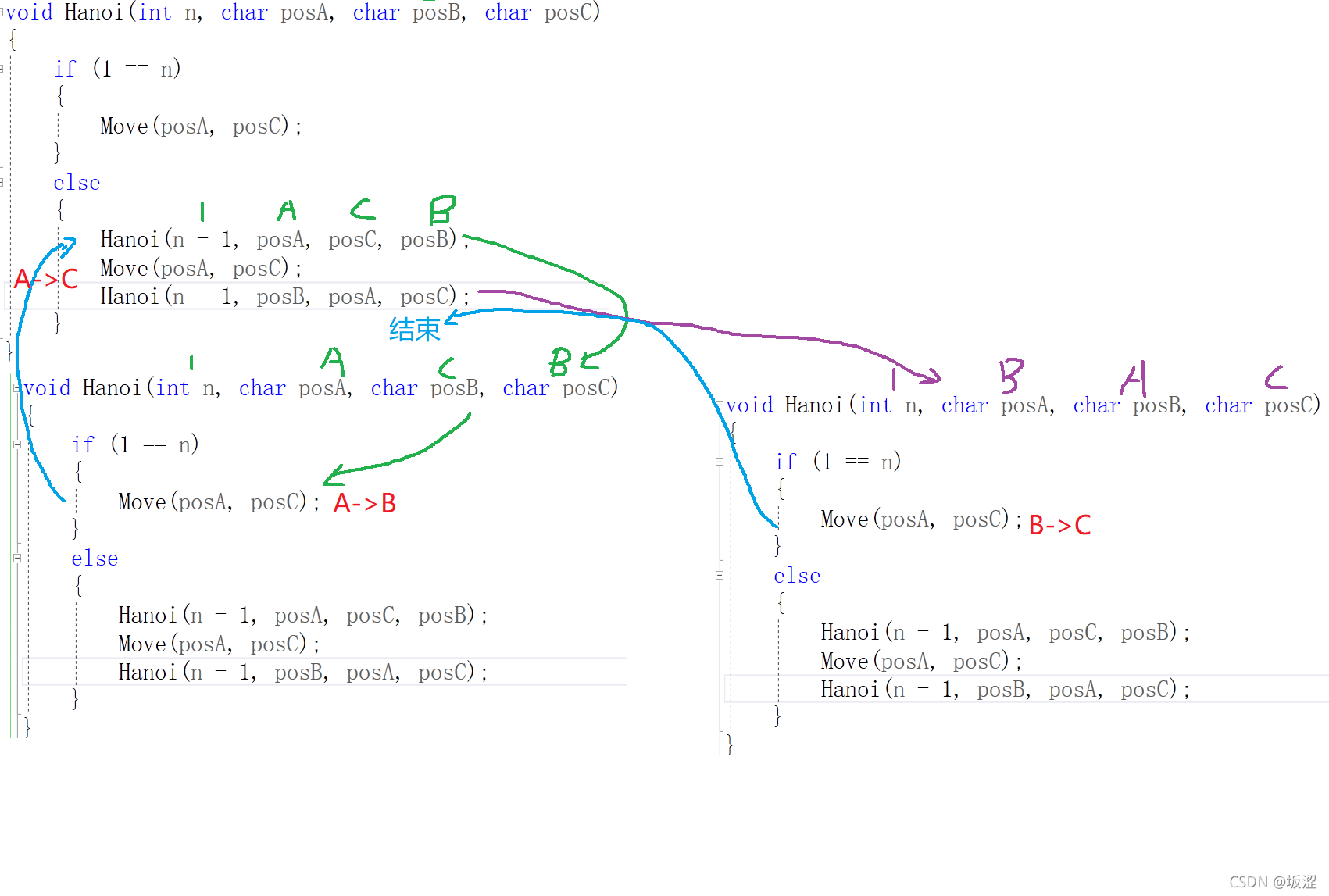
n=3或者n=n时和n=2也是大同小异,不管是多少层都当成2类看待,底层和底层以外的其他层.

 第一步,完成了第二层塔递归函数的步骤1,

第二步, 完成了第二层塔的函数,同时为第三层塔的步骤1进行了准备

 这是完成了第三层塔的步骤2. 我们可以发现接下来要进行第三层塔的步骤3,这个步骤就是将B上的塔放到C上,和两层塔的移位原理相同.(就当4层塔和3层塔不存在,挪动1,2层塔)

完成第3层塔 的步骤3,同时为第4层塔完成了步骤1接下来只要进行第4层塔的步骤2和步骤3就可以了.

总结

步骤1作用是将除底层的塔搬到中转位置,利用递归知道n减到1,将第一层搬走,然后退出函数进行步骤2,,将第二层搬到前两层塔的终止位置,步骤3将第一层塔与第二层塔摞在一起,为第三层塔的搬运做准备.

汉诺塔的理解比较抽象,如果想很好的理解,需要观察每移动一层塔的步骤,找到规律,才能很好的理解递归.