kmp 算法

KMP 相关题目

1. 28. 实现 strStr()

2. 459. 重复的子字符串

3. 686. 重复叠加字符串匹配

基本思想

KMP 算法是字符串匹配中经典算法，由 Knuth，Morris 和 Pratt 发现，所以取了三位学者名字的首字母，叫做KMP 算法

以 28. 实现 strStr() 为例

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

我们普通人的暴力破解思路：

func strStr(haystack string, needle string) int {
	if len(needle) == 0 {
		return 0
	}
	for i := 0; i <= len(haystack) -len(needle); i ++ {
		j := 0
		for ; j < len(needle); j ++ {
			if haystack[i + j] != needle[j] {
				break
			}
		}
		if j == len(needle) {
			return i
		}
	}
	return -1
}

这个解法在 Leetcode 能通过，但显然不是出题人所希望的答案

暴力思路：

• 当匹配不成功，haystack 从开始匹配的位置后移一位，与 needle 开始重新匹配

KMP 思路：

• 当匹配不成功时，其前面的字符已经匹配成功了，这里面就包含一定的信息，可以让字符匹配的位置不从头开始了

如下例子：

可以看到使用 KMP 算法可以大幅优化字符串匹配比对次数，不过 kmp 算法能够优化关键在于最长相等前缀后缀，在上述例子中就是 ABB

因此 KMP 算法中最关键的 Next 数组其实就是保存最长相等前缀后缀这个信息的, 以 ABBCABBD 为例

i	子字符串	前缀	后缀	next[i]
0	A	“”	“”	0
1	AB	[A]	[B]	0
2	ABB	[A,AB]	[B,BB]	0
3	ABBC	[A,AB,ABB]	[C,BC,BBC]	0
4	ABBCA	[A,AB,ABB,ABBC]	[A,CA,BCA,BBCA]	1
5	ABBCAB	[A,AB,ABB,ABBC,ABBCA]	[B,AB,CAB,BCAB,BBCAB]	2
6	ABBCABB	[A,AB,ABB,ABBC,ABBCAB]	[B,BB,ABB,CABB,BCABB,BBCABB]	3
7	ABBCABBD	[A,AB,ABB,ABBC,ABBCABB]	[D,BD,BBD,ABBD,CABBD,BCABBD,BBCABBD]	0

假设我们已经计算出了上述 NEXT 数组，回溯过程为：

• 假设在 ABBCABBD 最后位置 len(needle) - 1 即 D字符处匹配失败
• 回溯到 Next[len(needle) - 2] 指向的位置比较，即 needle 从 字符串位置 3 的字符 C开始比较

匹配过程如下：

func strStr(haystack string, needle string) int {
	if len(needle) == 0 {
		return 0
	}
	// 计算 Next 数据
	next := getNext(needle)
	j := 0
	for i := 0; i < len(haystack); i ++ {
		// 如果字符不匹配, 两种情况: 1. j 回溯匹配 2. j == 0, 则跳出此循环 i ++ 再来匹配 
		for haystack[i] != needle[j] {
			if j == 0 {
				break
			}
			// j 回溯 next[j-1] 的位置比较
			j = next[j - 1]
		}
		// 字符匹配上了：j++
		if haystack[i] == needle[j] {
			j ++
		}
		if j == len(needle) {
			return i - j + 1
		}

	}
	return -1
}

那 Next 数组如何构建？

• 遍历 needle 所有 i 位置的所有前缀后缀，计算最长相等长度

func getNext(needle string) []int {
	next := make([]int, len(needle))
	for j := 1; j < len(needle); j++ {
		max := 0
		// 遍历 i 的所有前后缀，找出最长相等的
		for l := 1; l <= j; l ++ {
			prefix := needle[0:l]
			suffix := needle[j-l+1:j + 1]
			if prefix == suffix {
				if l > max {
					max = l
				}
			}
		}
		next[j] = max
	}
	return next
}

显然上述计算两层循环复杂度太高

假设Next[i-1]=j 即 j 为最长相等前后缀长度，即 j 位置指向的字符则是下一个匹配的字符，Next[i] 的取值有以下情况：

1. 若 needle[j] == needle[i], 则 next[i] = j + 1

2. 若needle[j] != needle[i], j 需要回溯j = next[j-1] 处重新比较 j 与 i 处的字符串是否相等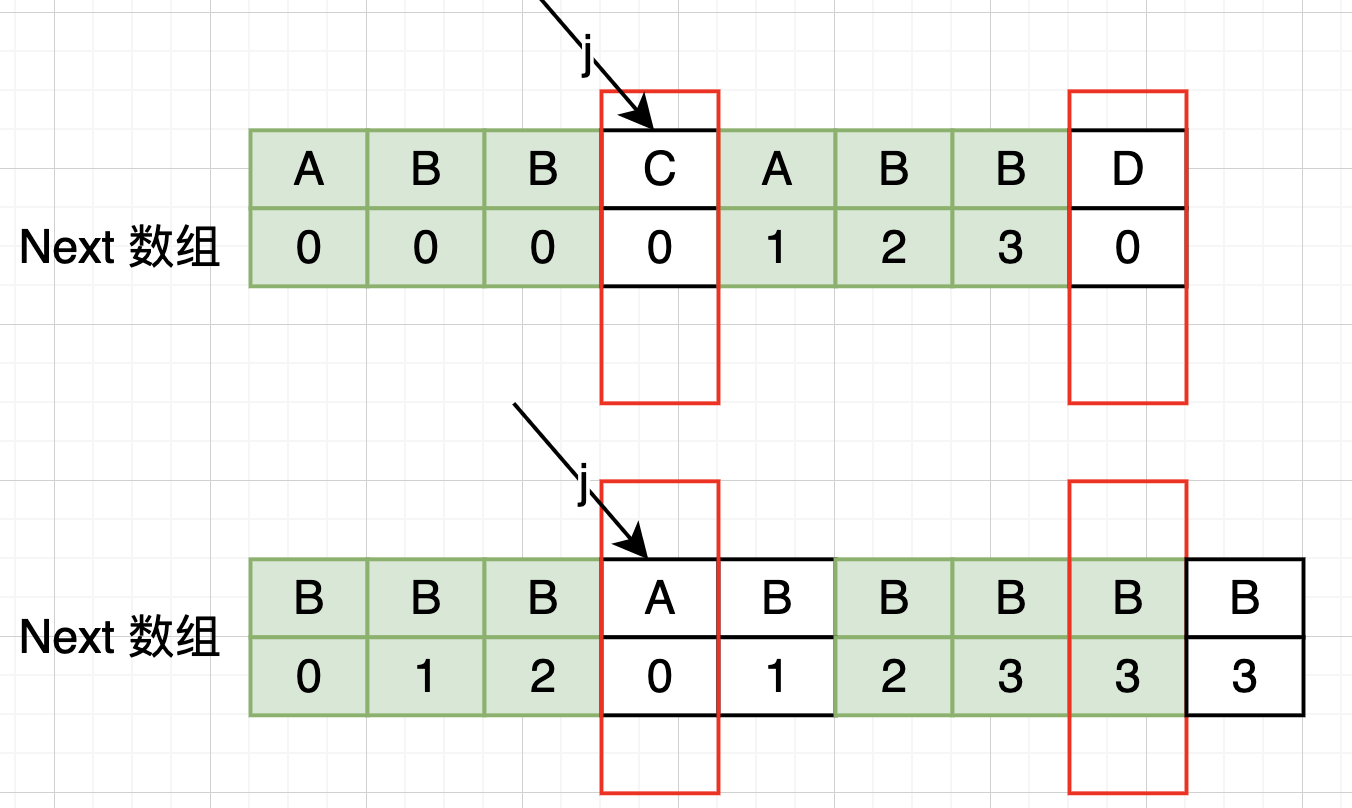

   

因此完整getNext(needle string)[]int方法为：

func getNext(s string) []int {
	next := make([]int, len(s))
	j := 0
	next[0] = j
	for i := 1; i < len(s); i ++  {
		for j > 0 && s[i] != s[j] {
			j = next[j-1]
		}
		if s[i] == s[j] {
			j ++
		}
		next[i] = j
	}
	return next
}

总结

leetcode 28 虽然只是个简单题，但仅仅在接受暴力解法时简单。kmp 算法比较复杂，并且在构建 next 数组 j 的回溯难以理解，应该多做几次，加强印象。

参考

http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html