算法7-7,7-8：无向图的连通分量和生成树

在对无向图进行遍历时，对于连通图，仅需从图中任一顶点出发，进行深度优先搜索或广度优先搜索，便可访问到图中所有顶点。对于非连通图，则需从多个顶点出发进行搜索，而每一次从一个新的起始点出发进行搜索的过程中得到的顶点访问序列恰为其各个连通分量中的顶点集。
对于非连通图，每个连通分量中的顶点集，和遍历时走过的边一起构成若干棵生成树，这些连通分量的生成树组成非连通图的生成森林。
假设以孩子兄弟链表作为生成森林的存储结构，则生成非连通图的深度优先生成森林的算法可以描述如下：

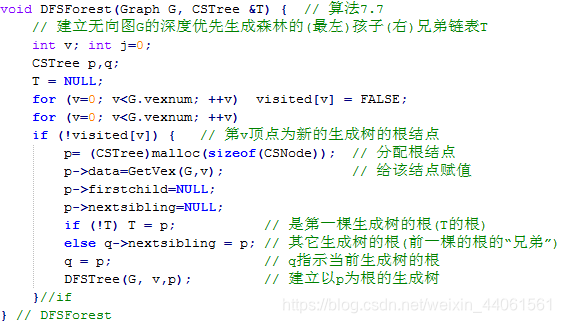
而建立以p为根的深度优先生成树的算法可以描述如下：

在本题中，读入一个无向图的邻接矩阵（即数组表示），建立无向图并按照以上描述中的算法建立无向图的生成森林。对于森林中的每一棵生成树，遍历所有顶点，并输出遍历顶点的顺序。

Input

输入的第一行包含一个正整数n，表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数0或1，对于第i行的第j个0或1，1表示第i个顶点和第j个顶点有直接连接，
0表示没有直接连接。当i和j相等的时候，保证对应的整数为0。
输入保证邻接矩阵为对称矩阵，即输入的图一定是无向图。

Output

每一行输出无向图中的一棵生成树，表示按照题目描述中的深度优先遍历算法遍历相应的连通分量的访问顶点顺序。
每个整数后输出一个空格，并请注意行尾输出换行。

Sample Input

6
0 0 0 1 0 0
0 0 1 1 0 0
0 1 0 1 0 0
1 1 1 0 0 0
0 0 0 0 0 1
0 0 0 0 1 0

Sample Output

0 3 1 2 
4 5 

Hint

在本题中，需要掌握图的深度优先遍历的方法，并需要掌握无向图的连通性问题的本质。
通过求出无向图的连通分量和对应的生成树，应该能够对图的连通性建立更加直观和清晰的概念。

#include<bits/stdc++.h>
using namespace std;
const int MAXN=100005;
int n,m,s