计算机视觉ch8 图像内容分类——基于KNN的手势识别

KNN算法原理

KNN即K最近邻，就是K个最近的邻居的意思，说的是每个样本都可以用它最接近的K个邻居来代表。KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。在分类中选择K个最相似数据中出现次数最多的分类作为新数据的分类，即“投票法”。它的核心思想可以用一句话来概括：物以类聚，人以群分。KNN算法主要涉及3个因素：样本集、距离或相似的衡量、K的大小。

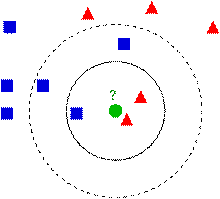
如上图，求绿色圆圈的所属类别，正方形和三角形都是样本数据。假设k=3，则绿色圆圈的邻居有两个三角形和一个正方形，按照投票法，绿色圆圈所属类别应该是红色三角形。若k=5，则绿色圆圈的邻居有两个三角形和三个正方形，则绿色圆圈所属类别是蓝色正方形
基本步骤

1. 计算测试对象和训练集每个对象之间的距离
2. 按递增顺序对距离进行排序
3. 把距离最近的K个点作为测试对象的最近邻
4. 找到这些邻居中的绝大多数类
5. 将绝大多数类返回作为我们对测试对象归属类的预测

用KNN实现简单分类

通过随机生成的方式，创建两个不同的二维点集class1和class2，每个点集有两类，分别是正态分布和绕环状分布，正态分布的范围主要通过代码中参数的调节实现，该参数越大，数据点范围越大，就更分散。

# -*- coding: utf-8 -*-
# 生成点的过程
from numpy.random import randn
import pickle
from pylab import *
# create sample data of 2D points
# 打印两百个点
n = 200
# two normal distributions
# 两百个二维的点并通过*0.6限制他们的范围
class_1 = 0.8 * randn(n, 2)
class_2 = 1.0 * randn(n, 2) + array([5, 1])
# 给他们分标签
labels = hstack((ones(n), -ones(n)))
# save with Pickle
# with open('points_normal.pkl', 'w') as f:
# 把他们存进
with open('points_normal_test.pkl', 'wb') as f:
    pickle.dump(class_1, f)
    pickle.dump(class_2, f)
    pickle.dump(labels, f)
# normal distribution and ring around it
print("save OK!")
# 环状的数据
class_1 = 0.3 * randn(n, 2)
r = 0.5 * randn(n, 1) + 5
angle = 2 * pi * randn(n, 1)
class_2 = hstack((r