数据结构学习，哈希表（HashTable）（java语言）

最新推荐文章于 2024-06-03 10:38:23 发布

收纳空白_

最新推荐文章于 2024-06-03 10:38:23 发布

阅读量709

点赞数 1

CC 4.0 BY-SA版权

分类专栏：学习文章标签：哈希表 java 数据结构 hashtable

本文链接：https://blog.youkuaiyun.com/weixin_44058809/article/details/88604407

学习专栏收录该内容

11 篇文章

订阅专栏

本文深入探讨哈希表原理，涵盖哈希函数设计、冲突解决策略，包括链地址法、开放地址法及再哈希法，解析哈希表的高效查找与删除操作。

1.什么是哈希表

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。
给定表M，存在函数f(key)，对任意给定的关键字值key，代入函数后若能得到包含该关键字的记录在表中的地址，则称表M为哈希(Hash）表，函数f(key)为哈希(Hash) 函数。

哈希表的实质是一个数组，不同的key通过哈希函数的转换得到一个索引值，在数组的索引处就是存放value的地方
例如：https://blog.youkuaiyun.com/weixin_44058809/article/details/88559457
这个leetcode 387题我们用到的思路2之中，我们创建了一个大小为26的哈希表，通过不同的字母（也就是哈希表的key）进行哈希函数运算（将key转化为索引），从而得到哈希表种对应索引处的值来巧妙的解决这一问题

2.哈希函数的设计

评判一个哈希表的好坏，关键就在于哈希函数的设计，一个好的哈希函数能最大限度的使我们存入的数据的key值经过哈希函数运算之后尽可能的平均分布在哈希表之中。

首先，一个哈希函数需要将不同的数据都转化成索引，就需要对数据进行处理，先说说对一些数据的处理方法

2.1整型

一般来说，整型可以直接使用

2.2大整数

对于大整数来说，我们可以将大整数模一个素数，这个素数也就是哈希表的容量

为什么要模素数？因为如果我们模一个合数，很容易出现哈希冲突，导致分布不均匀

2.3浮点型

对于浮点型的数据，我们可以将浮点型转化成对应的二进制数然后再对它进行素数取模

2.4字符串

对于字符串来说我们可以用以下公式设计哈希函数：
例如要对code进行哈希函数计算
hash(code) = (cB ^3 + oB ^2 + dB ^1 + eB ^0) % M
其中M为哈希表的容量，B为字符串中可能涉及到的字符的个数，例如只有26个小写字母，B就为26
如果用这个函数计算哈希值，当字符串长度很大，容易造成整型溢出，所以可以做出以下改良
hash(code) = (((c*B + o)*B + d)B + e) % M
这样设计的哈希函数还是容易造成整型溢出，所以我们还可以做出以下改良
hash(code) = ((((c%M)B + o)%MB + d)%MB +e)%M 这几种方法得到的模都相同

2.5复合型

与字符串型一样
hash(code) = ((((c%M)B + o)%MB + d)%M*B +e)%M

3.哈希冲突

当我们的数据不断存入哈希表，一定会出现哈希冲突，什么是哈希冲突呢？
哈希冲突就是当们对不同的key代入哈希函数运算时，得到的结果却相同，即：
hash(key1) == hash(key2)
例如我们有一个容量为3的哈希表
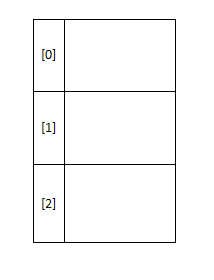
在这里插入图片描述
我们将2，5分别放入表中，如果我们的哈希函数是 x mod 3
首先 2 mod 3 = 2 ，我们放入hashtable[2]中，

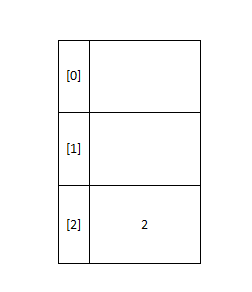
再将5放入，5 mod 3 = 2，我们放入hashtable[2]中，但是这里已经被使用了，这就出现了哈希冲突

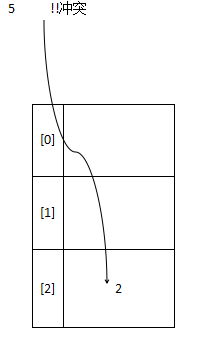
4.哈希冲突的解决方法

首先，不论哈希函数设计的多么巧妙，哈希冲突永远无法避免，所以我们要设计的哈函数应该尽可能使存入的数据平均分布在哈希表中，所以当冲突出现时，我们需要寻找一些解决方法

4.1链地址法：

链地址法即将哈希表中的每一个空间都放上一个链表，也可以理解为是一个链表的数组
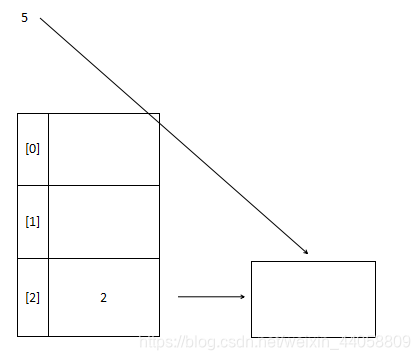
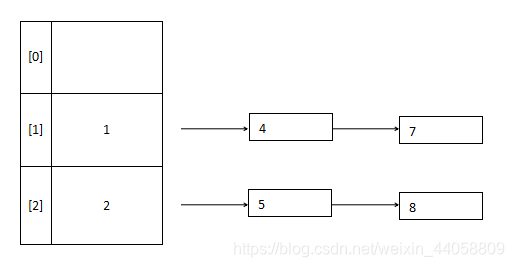
在这里插入图片描述

同样的，除了使用链表，我们还可以使用树结构等等

4.2开放地址法

如果我们要将8加入以下哈希表中，哈希函数是x mod 7，同样的出现了哈希冲突
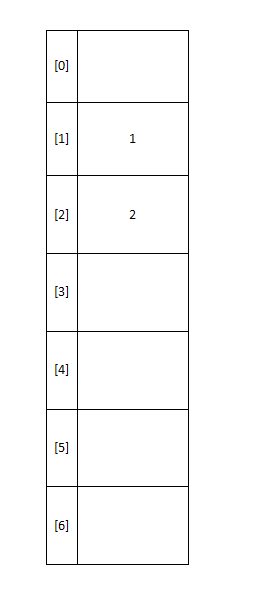
在这里插入图片描述

4.2.1线性探测

线性探测就是探测空白的单元，例如我插入一个元素8，mod 7 得到索引为1，此时1被占用，我们就将索引+1，即存到索引为2的位置，2也被占用，就再+1，得到索引为3，此时索引为3的位置是空的，就可以加入。
除了步长为1 之外，我们还可以设置步长为2，4…等等

4.2.2二次探测

二次探测与线性探测相同，只是此时的步长是一个动态的步长，先+1，再+4，再+9，等等，一直到找到第一个为空的位置时插入，由于每次都使用原始步长的平方，故称二次探测

4.3.3再哈希法

再哈希法即将key用另外的一个哈希函数再进行一遍计算，用得到的结果当作步长，这样做的好处是对于不同的key，得到的步长是不同的，对于相同的key，得到的步长是相同的，较于线性探测与二次探测来说，连续出现哈希冲突的概率更低，因此在使用开放地址法时，我们通常使用的是再哈希法

5.总结

哈希表的查找：当我们要在哈希表中查找一个key时，首先通过hash函数找到对应的索引，再通过key与value的一一比对判断是否是我们需要找的内容；
哈希表的删除：当使用链地址法时，删除一个元素很容易，直接在对应的链表中删除元素就好了，如果我们使用的是开放地址法就要担心了，因为在使用开放地址法的删除一个元素的时候，可能会导致后面的元素丢失了，为了解决这个问题，我们一般在删除了一个元素之后，在被删除位置添加上一个不可能存在的元素例如-1。