【Leetcode】计算中位数（数据流、滑动窗口、两个正序数组）

最新推荐文章于 2025-03-27 16:06:09 发布

原创最新推荐文章于 2025-03-27 16:06:09 发布 · 1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #java

算法分析专栏收录该内容

69 篇文章

订阅专栏

本文探讨了如何通过设计数据结构解决剑指Offer中的数据流中位数问题，包括使用堆的数据结构，以及如何处理滑动窗口中的中位数计算。还介绍了寻找两个正序数组中位数的高效算法，利用二分查找和插入排序。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

剑指 Offer 41. 数据流中的中位数

1. 题目描述

leetcode链接：剑指 Offer 41. 数据流中的中位数
在这里插入图片描述

2. 思路分析

设计两个堆，一个大顶堆，一个小顶堆，大顶堆用来存储小的一半数，小顶堆用来存储大的一半数。如果是奇数个数，则输出小顶堆的堆顶数据，如果是偶数个数，则输出小顶堆和大顶堆堆顶数的平均值。

3. 参考代码

class MedianFinder {
    PriorityQueue<Integer> queue1;
    PriorityQueue<Integer> queue2;

    /** initialize your data structure here. */
    public MedianFinder() {
        queue1 = new PriorityQueue<>();  // 小顶堆，保存大的一半
        queue2 = new PriorityQueue<>((a, b) -> (b - a));   // 大顶堆，保存小的一半
    }
    
    public void addNum(int num) {
        if (queue1.size() != queue2.size()) {
            queue1.offer(num);
            queue2.offer(queue1.poll());
        } else {
            queue2.offer(num);
            queue1.offer(queue2.poll());
        }
    }
    
    public double findMedian() {
        return queue1.size() == queue2.size() ? (queue1.peek() + queue2.peek()) / 2.0 : queue1.peek();
    }
}

480. 滑动窗口中位数

1. 题目描述

leetcode链接：480. 滑动窗口中位数
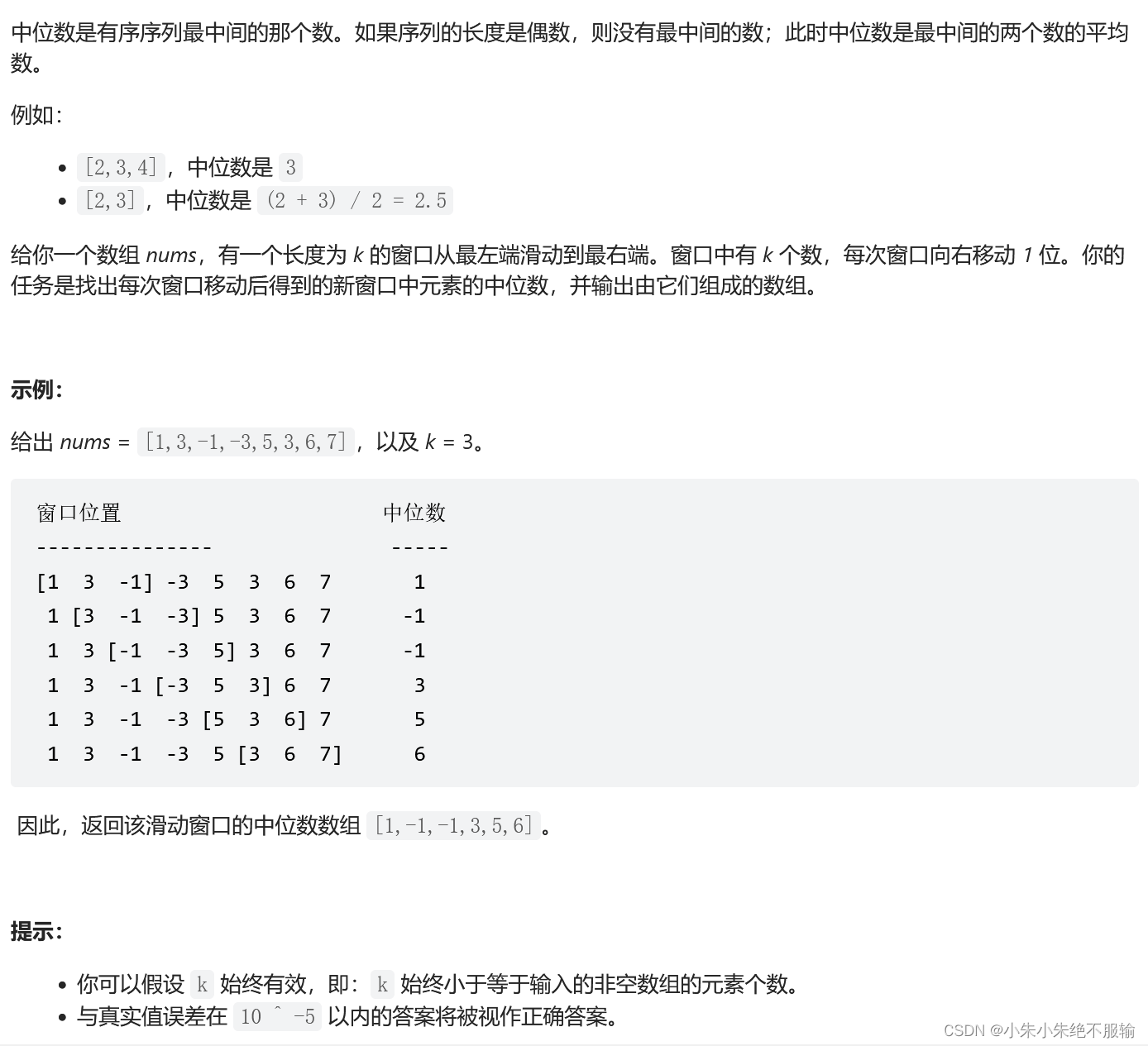
在这里插入图片描述

2. 思路分析

方法一：优先队列

根据上一题数据流的中位数，设置两个堆，一个大顶堆，一个小顶堆。需要注意的是，在堆中删除数据时要维护两个堆的大小平衡。

在Java代码中，需要注意：

大根堆初始化的时候用Integer.compare(b, a)，不要使用b - a，否则会溢出。
在计算中位数的时候，return ((double)A.peek() + B.peek()) / 2.0;，否则对于输入[2147483647,2147483647] 2会计算错误。

方法二：二分查找+插入排序

用插入排序维护一个窗口，每次插入数据时使用二分查找寻找插入位置。保证list是有序的，即滑动窗口有序。然后计算滑动窗口内的中位数。

3. 参考代码

方法一：优先队列

class Solution {
    PriorityQueue<Integer> A;  // 小顶堆
    PriorityQueue<Integer> B;  // 大顶堆
    public double[] medianSlidingWindow(int[] nums, int k) {
        A = new PriorityQueue<>();
        B = new PriorityQueue<>((a, b) ->(Integer.compare(b, a))); // -会溢出
        int n = nums.length;
        double[] res = new double[n - k + 1];
        for (int i = 0; i < n; i++) {
            addNum(nums[i]);
            if (i < k - 1) continue;
            res[i - k + 1] = getMedium(k);
            delNum(nums[i - k + 1], k);
        }
        return res;
    }
    public void addNum(int num) {
        if (A.size() != B.size()) {
            A.offer(num);
            B.offer(A.poll());
        } else {
            B.offer(num);
            A.offer(B.poll());
        }        
    }
    public void delNum(int num, int k) {
        if(B.contains(num)) {
            B.remove(num);
            if(k % 2 == 1) B.offer(A.poll());
        }else {
            A.remove(num);
            if(k % 2 == 0) A.offer(B.poll());
        }
    }
    public double getMedium(int k) {
        if (k % 2 == 0) {
            return ((double)A.peek() + B.peek()) / 2.0;
        } else {
            return (double)A.peek();
        }
    }
}

可以联想到【leetcode】滑动窗口的最大值。

方法二：二分查找+插入排序

class Solution {
    public double[] medianSlidingWindow(int[] nums, int k) {
        // 插入排序维护窗口，二分查找寻找插入位置
        List<Integer> list = new ArrayList<>();  // 存储滑动窗口的值
        int n = nums.length;
        double[] res = new double[n - k + 1];
        for (int i = 0; i < n; i++) {
            int pos = binarySearch(nums[i], list);
            list.add(pos, nums[i]);  // 将值插入滑动窗口
            if (list.size() < k) continue;
            if(k % 2 == 0) {
                res[i + 1 - k] = ((double)list.get(k / 2 - 1) + list.get(k / 2)) / 2;
            }else {
                res[i + 1 - k] = (double)list.get(k / 2);
            }
            list.remove((Integer)nums[i + 1 - k]);
        }
        return res;
    }
    public int binarySearch(int num, List<Integer> list) {
        int left = 0, right = list.size() - 1;
        while (left <= right) {
            int mid = (right - left) / 2 + left;
            if (list.get(mid) <= num) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }
}

4. 寻找两个正序数组的中位数

1. 题目描述

leetcode链接：4. 寻找两个正序数组的中位数
在这里插入图片描述

2. 思路分析

二分查找

题目的要求时间复杂度应该为O(log(m + n))，所以常规的方法是不满足条件的，需要使用二分查找。

可以参考：【Leetcode】二分法问题解析（模板+应用）

3. 参考代码

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        int left = (m + n + 1) / 2;
        int right = (m + n + 2) / 2;
        return (findK(nums1, 0, nums2, 0, left) + findK(nums1, 0, nums2, 0, right)) / 2.0;
    }
    public int findK(int[] nums1, int i, int[] nums2, int j, int k) {
        int m = nums1.length, n = nums2.length;
        if (i >= m) return nums2[j + k - 1];  // nums1为空数组
        if (j >= n) return nums1[i + k - 1];  // nums2为空数组
        if (k == 1) {
            return  Math.min(nums1[i], nums2[j]);
        }
        int mid1 = (i + k / 2 - 1 < m) ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;
        int mid2 = (j + k / 2 - 1 < n) ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;
        if (mid1 < mid2) {
            return findK(nums1, i + k / 2, nums2, j , k - k / 2);
        } else {
            return findK(nums1, i, nums2, j + k / 2 , k - k / 2);
        }
    }
}