排序是数据结构中很重要的算法, 说起来是算法, 个人感觉也就是种思想,明白每种算法的设计思想。 就很简单了。
算法最忌讳死记硬背。 所以对于算法静下心来,慢慢来, 多思考多分析。这样才扎实,在以后算法的扩展, 算法的优化才能更加轻松。
一、冒泡排序
给我们的一组序列{ 25,6,56,24,9,12,55 } , 长度为7。

看着上图, 我们分析分析, 我们共执行了6次(也就是n-1)趟排序。
每一趟排序都是将一个最大值放到合适的位置, 例如第一趟排序,56放到合适位置。当放合适的位置后, 下一趟排序就不管它。
第二趟排序, 55放到合适的位置。
第三趟排序, 25放到合适的位置。
直到第6趟排序, 我们把所有元素都放到合适的位置 - 即排序完毕。
总结出的思想就是: 长度为n的数组, 我们共需要n-1趟排序。
对于每一趟我们都会将一个最大值放到合适的位置。
基于这样的思想, 我们设计代码, 我们可以使用嵌套的for循环去做。
外循环是控制n-1趟排序, 内循环是一趟排序筛选最大值放到合适的位置。
void Bubble_Sort(int* a, int lengh) {
if (!a) {
return;
}
for (int i = 0; i < lengh - 1; i++) {
for (int j = 0; j < lengh - i - 1; j++) {
if (a[j] > a[j + 1]) {
std::swap(a[j], a[j + 1]);
}
}
}
}
int main() {
int a[10] = { 10,9,8,7,6,5,4,3,2,1 };
int lengh = sizeof(a) / sizeof(a[0]);
Bubble_Sort(a, lengh);
return 0;
}
上面的代码就是一个冒泡排序的实现, 但是这个代码写的不完美, 也不好。
为什么呢? 因为没有优化, 一般来说冒泡排序的时间复杂度为o(n^2),是很慢的。
void Bubble_Sort(int* a, int lengh) {
if (!a) {
return;
}
for (int i = 0; i < lengh - 1; i++) {
int flag = 0; //优化器
for (int j = 0; j < lengh - i - 1; j++) {
if (a[j] > a[j + 1]) {
std::swap(a[j], a[j + 1]);
flag = 1; //当发生交换,意味着没有排序好, 我们把falg置为1.
}
}
if(flag == 0) { //flag为0代表着已经排序好了
return;
}
}
}
但是当我们优化之后它的效率会得到提升。也就是上面,只是加一个优化器flag。
对于这个案例: { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }已经排序好的序列。
未优化的时间复杂度还是o(n^2), 但是优化后的时间复杂度为o(n)。
分析冒泡排序性能。
a、时间复杂度为:o(n^2), 空间复杂度为:o(1)。
b、不加优化器flag, 最坏性能~最佳性能:[ o(n^2) ~ o(n^2) ]。
c、加优化器flag, 最坏性能~最佳性能: [ o(n^2) ~ o(n) ] 。
d、冒泡是一种稳定的排序。
(何为稳定性? 举个例子, 【5A, 6, 5B】这个序列,5A和5B都是5,作为区分5我用A、B。 如果排序后5A还是在5B的前面, 也就是两个5的相对位置没有发生改变,则稳定性好。 如果相对位置发生变化。则为不稳定 )
二、直接插入排序
当插入一个新的元素时, 前面的序列已经排序好,这个新元素会和前面的序列进行比较,最终放到合适的位置, 使得新的序列为新的排序好的序列。

就跟玩扑克牌一样, {2,4,5,10}已经排序好的, 新插入的元素为7, 我们把7插入合适的位置,然后新的序列为 {2,4,5,7,10}。
在这里我提供两种写法。
//直接插入排序写法1
void Insert_Sort1(int* a, int lengh) {
if (!a) {
return;
}
for (int i = 0; i < lengh - 1; ++i) {
int end = i;
int tmp = a[end + 1];
while (end >= 0 && a[end] > tmp) {
a[end + 1] = a[end];
--end;
}
a[end + 1] = tmp;
}
}
//直接插入排序写法2
void Insert_Sort2(int* a, int lengh) {
if (!a) {
return;
}
for (int i = 0; i < lengh - 1; i++) {
int end = i;
while (end >= 0 && a[end] > a[end + 1]) {
std::swap(a[end], a[end + 1]);
--end;
}
}
}
这两种写法都是插入的元素在原来排序的序列中进行重新排序。
说实话第一种写法是我以前学的时候老师写的, 第二种写法是自己看完思想自己写的。 第一种写法没有第二种写法好理解。两种算法都是基于一个思想实现, 不过是设计不同罢了。 时间复杂度都差不多。
分析直接插入排序性能:
a、时间复杂度为o(n^2), 空间复杂度为o(n^2)。
b、最差性能~最优性能: [ o(n^2) ~ o(n^2) ]。
c、直插排序是稳定排序。
三、选择排序

从上面的算法思想图可以看出, 每一趟都会从待排序的序列挑选最小值放到合适的位置。 是不是和冒泡排序有相同之处呢。
void Select_Sort(int* a, int lengh) {
if (!a) {
return;
}
for (int i = 0; i < lengh - 1; i++) {
int index = i;
for (int j = i + 1; j < lengh; ++j) { //查找最值下标
if (a[j] < a[index]) {
index = j;
}
}
if (index != i) {
std::swap(a[i], a[index]);
}
}
}
但还是和冒泡排序有区别的, 选择在寻找最值的时候重点是放在查找最值的下标。
最终通过判断该下标和i下标是否相同。如果相同代表i下标就是最值。否则就是最值在后面的。交换。
我个人对于选择排序的感觉, 一开始我不太看好这个算法, 因为时间效率不高, 稳定性还不好。但是算法的设计总是有价值的。 或许选择排序查找最值的方式就是它的价值。 冒泡查找最值的方式可能会存在多次swap交换。 而选择排序只是找最值的下标。 如果交换的代价是很大的。 这个时候冒泡就会不如选择排序了, 当然如果只是一些简单的排序交换代价不大,个人感觉冒泡和直插还是优于选择排序的。
分析选择排序:
a、时间复杂度为:o(n^2), 空间复杂度为: o(1)
b、最差效率~最优效率: [ o(n^2) ~ o(n^2) ]。
c、选择排序是不稳定排序。
四、希尔排序

希尔排序是直接插入排序的升级版。从上图可以看出。
从上的排序中我们可以看出共分为3趟排序。
gap=5, 每个元素间隔为5,进行排序。
gap=3, 每个元素间隔为3, 进行排序。
gap=1, 即每个元素间隔为1, 进行最终一趟排序。
你可以看出每趟希尔排序有很多小直接插入排序。 当gap=1的时候,就是一次完整直接插入排序。
这可能是大家困惑的问题, 它里面包含那么多直插排序, 怎么可能性能比直接插入排序性能好呢?
1、首先我们先要明白直接插入的缺点和如何提升直插的效率。 我们发现当序列大多的是有序有规律的时候, 直插的效率会很高。 例如【2,3,4,5】序列中新插入元素1,这个元素1需要不断和前面的元素进行比较,最终在2这号位置插入1。 这个效率为o(n); 我们再来看看这个【2,3,4,6】序列新插入元素5, 我只需要一次比较,在6这个位置插入5即完毕。
9, 1, 2, 5, 7, 4, 8, 6, 3, 5
这是开始的数据, 你可以试试直接用直接插入排序去做。
2, 1, 4, 3, 5, 6, 5, 7, 8, 9
这是希尔排序微调后的序列,你再试试调用直接插入排序去做。
你会发现第二个序列速度比第一个序列快的不只是一点。
2、当gap=5的时候,我们会有5组数据,每组数据很少,上图为2个, 2个数据调用直插排序是很快的。 当gap=5微调结束后。 这个序列就会变得理想很多。再gap=2直插浪费的时间也不会很多。 最终gap=1时这个序列非常理想。 我们都知道理想的序列调用直插最大性能可以达到o(n)。
当然通过上面我所说的,我想你已经明白为什么希尔排序最佳性能为o(n^1.3), 不是n了, (因为存在gap=5,gap=2的微调, 即使给我们一个有序的序列我们还是会微调,这些微调会浪费时间)。因此希尔排序并不是一定会比直插排序好。 我们得看序列的理想成度。(当为有序的序列, 希尔不如直插!)
基于直接插入排序我写了两种写法, 这里我也会给两种希尔的写法。
//希尔写法1
void Hill_Sort(int* a, int lengh) {
if (!a) {
return;
}
int gap = lengh;
while (gap > 1) {
gap = gap / 2;
if (gap == 0) {
gap = 1;
}
for (int k = 0; k < gap; ++k) {
for (int i = k; i < lengh - gap; i += gap) {
int end = i;
int tmp = a[end + gap];
while (end >= k && a[end] > tmp) {
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = tmp;
}
}
}
}
//希尔写法2
void Hill_Sort1(int* a, int lengh) {
if (!a) {
return;
}
int gap = lengh;
while (gap > 1) {
gap = gap / 2;
if (gap == 0)
gap = 1;
for (int k = 0; k < gap; ++k) {
for (int i = k; i < lengh - gap; i++) {
int end = i;
while (end >= k && a[end] > a[end + gap]) {
std::swap(a[end], a[end + gap]);
end -= gap;
}
}
}
}
}

两个写法我自测过, 一样的结果。关于两个写法的优略性。
我做一些分析, 写法1重在赋值, 写法2重在交换。 交换理解可以分解为3次赋值。
因此重点就在于赋值上面。这得看赋值的代码大不大了? 一般来说算法赋值没有大太大代价, 两者近乎相等。
分析希尔排序:
a、时间复杂度为:o(n*log2^n) ~ o(n^2), 空间复杂度为:o(1)。
b、最差效率~最佳效率: [ o(n^2) ~ o(n^1.3) ]。
c、希尔排序是不稳定排序。
五、快速排序
基本思想:在序列中给我们一个基准值, 我们将该序列分割–把小于基准值的值放到基准值的左边称为左序列, 把大于基准值的值放到基准值的右边称为右序列。 左序列、右序列再次分割。 可以看出分割一次会有一个元素放到合适的位置。
我们的分割可是2^n倍率分割哦, 所以很快的。 这个思想类似于二叉树。
原序列为: [ 49, 38, 65, 97, 76, 13, 27, 49 ]

看着原序列, 我们以49为基准, 进行一次分割, 对于分割后的序列我们再以27, 76为基准进行二次分割。 最终我们再以13, 38,49,97为基准分割。 基准值的选取为序列的头元素。
由于基于二叉树的思想去设计, 因此我们的实现会有两种:一种是递归, 另一种是迭代(非递归)。
int Part_Find(int* a, int left, int right) {
if (!a) {
exit(0);
}
int key = a[left];
while (left < right) {
while (left < right && a[right] >= key) {
--right;
}
a[left] = a[right];
while(left < right && a[left] <= key) {
++left;
}
a[right] = a[left];
}
a[left] = key;
return left;
}
//递归实现
void Fast_Sort(int* a, int left, int right) {
if (!a) {
return;
}
if (left >= right) {
return;
}
int mid_index = Part_Find(a, left, right);
Fast_Sort(a, left, mid_index - 1);
Fast_Sort(a, mid_index + 1, right);
}
//非递归实现
void Fast_Sort1(int* a, int left, int right) {
if (!a) {
return;
}
if (left >= right) {
return;
}
queue<int> qe;
qe.push(left);
qe.push(right);
while (!qe.empty()) {
int begin = qe.front();
qe.pop();
int end = qe.front();
qe.pop();
int mid_index = Part_Find(a, begin, end);
if (begin < mid_index - 1) {
qe.push(begin);
qe.push(mid_index - 1);
}
if (mid_index < end) {
qe.push(mid_index + 1);
qe.push(end);
}
}
}
上面的迭代写法是比较好理解的,你既可以使用栈去做, 又可以使用队列去做。
只不过是保存left,right而已。
我们来分析下影响快速排序性能的原因。
1、基准值选取的不合理, 基准值是作为分割的, 如果选取不合理意味着分割不好。 最理想的分割是左序列的长度(小于基准值)等于右序列的长度(大于基准值的)。每一块序列都是这样的分割, 那么执行效率是最好的。 如果是分割的不均匀。 例如对一个有序序列进行分割。 你可以试试。 它的效率会非常差。 不如冒泡、直插排序。
对于这个问题, 我们采用三数取中法来选取最佳的基准值。 从而提升效率。
(所谓三数取中法 - begin,mid,end这三个下标对应的元素进行比较, 最终三个值的中间值作为基准值返回。)
2、在分割后序列长度很小时,我们不建议再使用递归去做了, 递归会有函数栈的开销。 我们建议序列很小时, 直接调用直接插入排序去做。减少函数栈的开销提升效率。
优化后的快速排序:
//三数取中法 -- 也就是找中间值。
int average_threevalues(int* a, int left, int right)
{
int mid = left + (right - left) / 2;
if (a[mid] > a[left])
{
if (a[mid] < a[right])
return mid;
else
{
if (a[left] < a[right])
return right;
else
return left;
}
}
else
{
if (a[left] < a[right])
return left;
else
{
if (a[mid] < a[right])
return right;
else
return mid;
}
}
}
int Part_Sort(int* a, int left, int right)
{
//优化1 -- 交换三数取中法返回的最佳基准
Swap(&a[left], &a[average_threevalues(a, left, right)]);
int key = a[left];
while (left < right)
{
while (left < right && a[right] >= key)
--right;
a[left] = a[right];
while (left < right && a[left] <= key)
++left;
a[right] = a[left];
}
a[left] = key;
return left;
}
void Fast_Sort(int* a, int left, int right)
{
if (!a)
return;
if (right - left + 1 < 5) //优化2 -- 长度小于5 -- 调用直插排序
{
Insert_Sort(a, left, right - left);
}
else if (left >= right)
{
return;
}
else
{
int mid = Part_Sort(a, left, right);
Fast_Sort(a, left, mid - 1);
Fast_Sort(a, mid + 1, right);
}
}
分析快速排序:
a、时间复杂度:o(n*log2^n) , 空间复杂度为: 递归实现o(log2^n), 非递归实现(o(1))
(递归会有函数栈的开销, 也算是空间代价)
b、最差效率~最佳效率: 【 o(n^2) ~ o(n * log(2^n) 】。
c、快速排序是不稳定排序。
六、堆排序
堆排序是利用二叉树线性存储设计的一种算法, 我在之前的文章有讲过。
https://blog.youkuaiyun.com/weixin_44024891/article/details/106796919
如果想要实现一个从小到大有序的序列。我们需要构建出来一个大根堆。
相反如果是从大到小有序的序列, 我们需要构建出来一个小根堆。
void ShiftDown(int* a, int node, int lengh) {
if (!a) {
return;
}
int parent = node;
int child = 2 * parent + 1;
while (child < lengh) {
if (child + 1 < lengh && a[child + 1] > a[child]) {
child++;
}
if (a[child] > a[parent]) {
std::swap(a[child], a[parent]);
parent = child;
child = 2 * parent + 1;
}
else {
return;
}
}
}
void BeHeap(int* a, int lengh) {
if(!a) {
return;
}
int last_leafnode = (lengh - 1) / 2;
for (int i = last_leafnode; i >= 0; i--) {
ShiftDown(a, i, lengh);
}
}
void Heap_Sort(int* a, int lengh) {
if(!a) {
return;
}
BeHeap(a, lengh); //构建大根堆
int size = lengh;
while (size > 1) {
std::swap(a[0], a[size - 1]);
--size;
ShiftDown(a, 0, size);
}
}
分析堆排序:
a、时间复杂度: o(n * log(2^n)), 空间复杂度: o(1)
b、最差效率~最佳效率: 【 o(n * log(2^n) ~ o(n * log(2^n) 】
c、 堆排序是不稳定排序。
七、归并排序
归并排序采用分治思想, 将序列分解成若干个小序列, 每个子序列有序, 然后每两两小序列合并排序成序列, 保证每个序列合并前是有序的,合并后也是有序的。
最后有序的子序列合并到一块, 整个序列都是有序的。
红色部分为分割, 蓝色部分为合并。
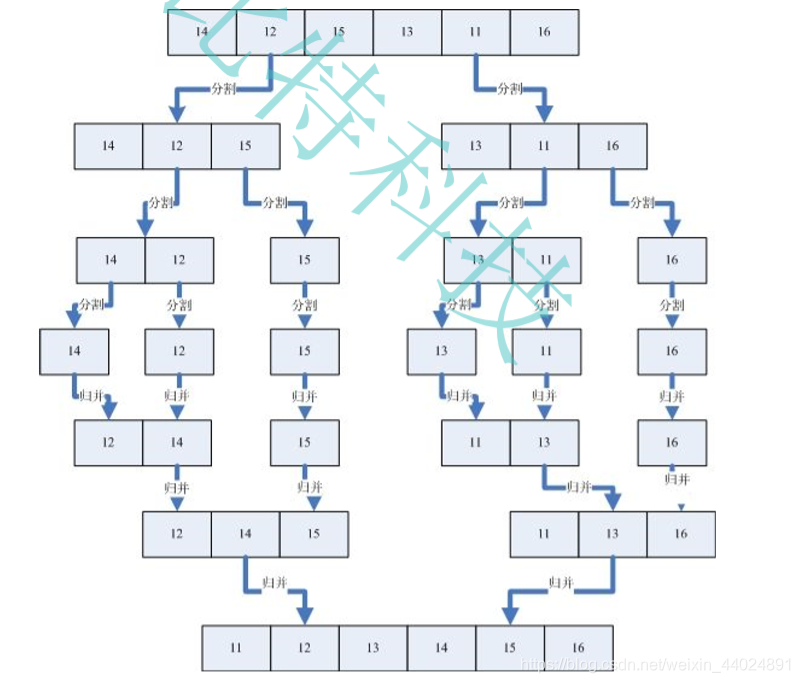
void Merge_Sort(int* a, int left, int right, int* tmp) {
//a为原数组, left其实下标, right尾下标, tmp为额外空间
if (!a) {
return;
}
if (left >= right) {
return;
}
int mid_index = left + (right - left) / 2;
Merge_Sort(a, left, mid_index, tmp);
Merge_Sort(a, mid_index + 1, right, tmp);
int begin1 = left, begin2 = mid_index + 1;
int end1 = mid_index, end2 = right;
int totoal_index = begin1;
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
tmp[totoal_index++] = a[begin1++];
}
else {
tmp[totoal_index++] = a[begin2++];
}
}
while (begin1 <= end1) {
tmp[totoal_index++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[totoal_index++] = a[begin2++];
}
while (left <= right) {
a[left] = tmp[left];
left++;
}
}
归并排序整体的性能都特别好, 要说不足那可能就是额外n空间开销吧。
归并排序可以一大块的序列, 划分很多块小块, 然后小块和小块之间排序组合,最终形成大块。
这种思想很适合我们排序磁盘上的数据, 因为我们内存空间是有限的。磁盘上的数据是很大的。
分析归并排序下:
a、 时间复杂度: o(n * log2^n), 空间复杂度为: o(n)
b、最坏效率~最佳效率: 【o(n * log2^n) ~ o(n * log2^n)】
c、 归并排序是稳定排序。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








