动态规划（装配线调度）

装配线问题：
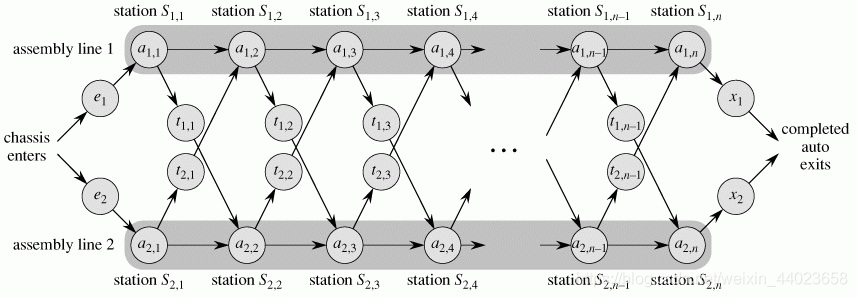
某个工厂生产一种产品，有两种装配线选择，每条装配线都有n个装配站。可以单独用，装配线1或2加工生产，也可以使用装配线i的第j个装配站后，进入另一个装配线的第j+1个装配站继续生产。现想找出通过工厂装配线的最快方法。

装配线i的第j个装配站表示为Si,jSi,j,在该站的装配时间是ai,j
如果从 Si,jSi,j装配站生产后，转移到另一个生产线继续生产所耗费的时间为ti,jti,j
进入装配线花费时间eiei,完成生产后离开装配线所耗费时间为xi

令f*表示通过生产所有路线中的最快的时间
令fi[j]fi[j]表示从入口到装配站Si,jSi,j的最快的时间.(i=1,2 ; j=1,2,…n;)

f1[1] = e1 + a1,1
f2[1] = e2 + a2,1
通过装配站S1,jS1,j的最快路线可能是通过S1,j−1站直接到S1,j，也可能是通过S2,j−1站，从装配线2到装配线1.
所以有递归公式：

动态规划思想
采用动态规划的前提：具有最优子结构和重叠子问题的性质。
在求解f1[n]和f2[n]的过程中，需要求解f1[n−1]和f2[n−1]，继续向前迭代计算…
即需要计算所有出所有的fi[j],i=0,1;j=1,2…n,此过程中需要不断的对同一个问题进行多次计算。
例如f1[n]的次数r1[n]为1,那么r1[n−1] =r1[n] +r2[n] ，r1[n−2] =r1[n−1] +r2[n−1] ，呈现指数增长，即ri[j]=2n−j
由上问题满足重叠的子问题的性质，
构成原问题的最优解由相关子问题的最优解组合而成，而这些子问题可以独立求解，即满足最优子结构。
动态规划的思想即安排求解顺序，对每个子问题只求解一次，并将结果保存下来，如果随后再次需要求此问题的解，只需要查找保存的结果，而不必重新计算

因为fi[j]fi[j]的值是由f1[j−1]和f2[j−1]决定，所以采用递增的站编号来计算fi[j]fi[j]，自底向上的方法。

例程

颜色深的线表示最快的装配路线
其中li[j]li[j],表示，到达装配线i的第j个装配站的最快路线的位置，值为1或2。
l*表示产品最后出自哪个装配线值为1或2

#include <cstdio>

int  f[2][6]={0};       //对应通过各个装配占的最短时间
int l[2][6]={0};        //对应通过各个装配占的来源
int __F;        //通过装配线最短时间
int __L;        //产品最终产出那个生产线

/*
    a[][]，每个站所需时间
    e[]最开始每条路线时间
    t[][]换线路所需时间
*/
void Fastest_way(int a[][6], int t[][5], int e[], int x[], int n)
{
    int j = 0;
    f[0][0] = e[0] + a[0][0];
    f[1][0] = e[1] + a[1][0];
    
    //自底向上开始计算f[i][j]的值，与[i][j]
    for(j = 1; j <n; j++)
        {
            //选0线开头
            if(f[0][j-1] + a[0][j] <= f[1][j-1] + t[1][j-1] + a[0][j])
            {
                f[0][j] = f[0][j-1] + a[0][j];
                l[0][j]= 0;
            }
            else
            {
                f[0][j] = f[1][j-1] + t[1][j-1] + a[0][j];
                l[0][j]= 1;
            }
            
            //选1线开头
            if(f[1][j-1] + a[1][j] <= f[0][j-1] + t[0][j-1] + a[1][j])
            {
                f[1][j] = f[1][j-1] + a[1][j];
                l[1][j]= 1;
            }
            else
            {
                f[1][j] = f[0][j-1] + t[1][j-1] + a[1][j];
                l[1][j]= 0;
            }
        }
        
        if(f[0][5] + x[0] <= f[1][5] + x[1])
           {
               _F = f[0][5] + x[0];
                _L = 0;
           }
        else
        {
                _F = f[1][5] + x[0];
                _L = 1;
        }
    }
    
void Print_Station(int l[][6], int __L, int n)
{
    //逆序输出
    int i = __L;
    printf("line %d, station %d\n", i+1,n);
    for(int j = n-1; j>=1; j--)
    {
        i = l[i][j];
        printf("line %d, station %d\n", i+1,j);
    }
    
    //正序输出
    if(n==0)
        return;
    __L = l[__L][n];
    Print_Station(l, __L, n-1);
    printf("line %d, station %d\n", l[__L][n]+1,n);
}

void main()
{
        int a[2][6]={{7,9,3,4,8,4},
                    {8,5,6,4,5,7}};
        int t[2][5]={{2,3,1,3,4},
                    {2,1,2,2,1}};
        int x[2]={3,2};
        int e[2]={2,4}; 

        Fastest_Way(a,t,e,x,6);
        Print_Station(l,__L,6);
}