最近在跟着Datawhale组队学习打卡,学习李宏毅的机器学习/深度学习的课程。
课程视频:https://www.bilibili.com/video/BV1Ht411g7Ef
开源内容:https://github.com/datawhalechina/leeml-notes
本篇文章对应视频中的P3。另外,最近我也在学习邱锡鹏教授的《神经网络与深度学习》,会补充书上的一点内容。
通过上一次课1.机器学习介绍,我们了解到机器学习分为3个步骤1)define a set of function;2)goodness of function;3)pick the best function。本篇文章主要介绍线性回归中的(1)损失函数、(2)梯度下降、(3)过拟合和正则化。
文章目录
1. 损失函数
目的:损失函数就是用来衡量模型好坏的,即预测值和真实值之间的差别。
偏倚 bias:模型预测值与真实值的差异,由于学习算法的错误或过于简单的假设造成的误差,它会导致模型欠拟合
1.1 线性回归模型的参数
对于一个线性回归的模型,有
y
=
b
+
∑
w
i
x
i
(1.1)
y = b+ \sum w_ix_i \tag{1.1}
y=b+∑wixi(1.1)
其中,
x
i
x_i
xi是各个特征,
w
i
w_i
wi是各个特征的权重,
b
b
b为偏移量,
y
y
y为预测值.
1.2 损失函数Loss Function的公式
损失函数的公式为
L
(
f
)
=
L
(
w
,
b
)
=
∑
n
=
1
10
(
y
^
n
−
f
(
x
c
p
n
)
)
2
(1.2)
L(f) =L(w,b)= \sum_{n=1}^{10}(\hat{y}^n-f(x_{cp}^n))^2 \tag{1.2}
L(f)=L(w,b)=n=1∑10(y^n−f(xcpn))2(1.2)
需要注意的是,这里的
x
n
x^n
xn与1.1式中的
x
i
x_i
xi不同。对于训练集中不同的样本,这里使用
x
1
,
x
2
,
.
.
.
,
x
n
x^1, x^2,...,x^n
x1,x2,...,xn 来表示每个样本的特征向量。
y
^
\hat{y}
y^为真实值。

1.3 f ∗ f^* f∗ 找出最好的function(最小二乘法)
我们需要找出损失函数值最小的function,并将其记为
f
∗
f^*
f∗ ,
f
∗
f^*
f∗的公式可见下图:
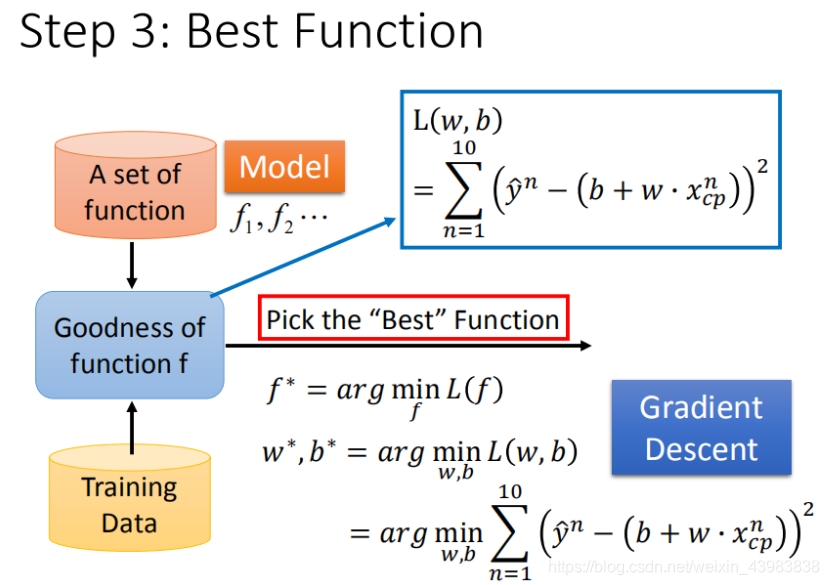
显然,为了找到
f
∗
f^*
f∗,我们需要找出满足
f
∗
f^*
f∗的最优解
w
∗
w^*
w∗和
b
∗
b^*
b∗。
在西瓜书中也有提到,基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。因此,我们可以将 L ( w , b ) L(w,b) L(w,b)分别对 w w w和 b b b求导,令求导式为0,则可以得到最优解 w ∗ w^* w∗和 b ∗ b^* b∗。
这里我公式推导一下用“最小二乘法”对
w
∗
w^*
w∗和
b
∗
b^*
b∗求解:

除了上述的最小二乘法,我们还可以用梯度下降的思想来求解最优的function的参数。
2. 梯度下降
目的:梯度下降就是要找出满足全局最优点的参数值。那么在只有一个参数的情况下,就是找出曲线的最低点,类似“下山”(因为损失函数的值越低越好)。
- 需要用到数学中的求导,偏微分,来接近参数 w w w取值的最优点。
- 如果斜率<0 , → \rightarrow → 右边损失函数的值更低, → \rightarrow → 因此要往右边走, → \rightarrow → 即 w w w增大(从 w 1 w_1 w1走到 w 2 w_2 w2)。
- 学习率learning rate:学习的步长(大:容易震荡;小:收敛慢)
- 在线性回归中没有局部最优,只有全局最优,所以目前不用考虑如何跳出局部最优。
因为线性回归是convex,即凸出的,只有一个最优点。
补充一个凸优化(convex optimation)的概念,感兴趣的同学可以看下 Stephen Boyd等人写的,王书宁等人翻译的《凸优化》。
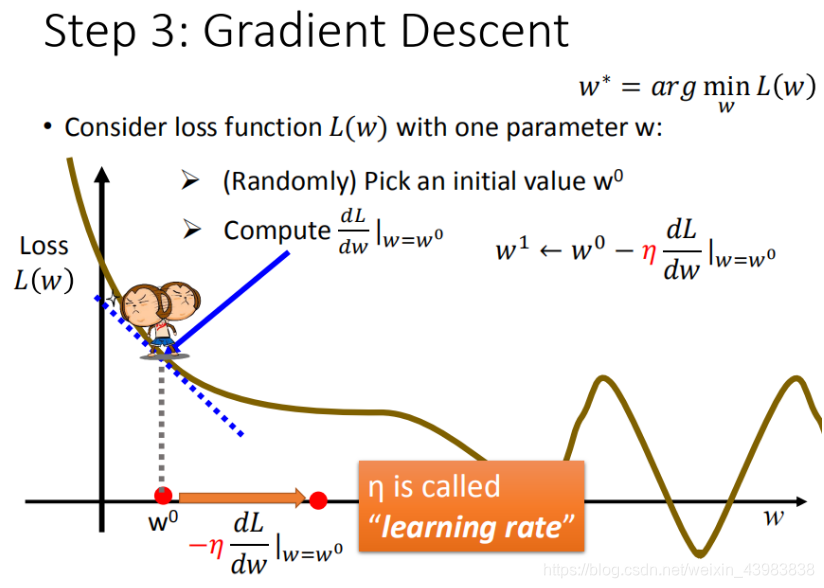
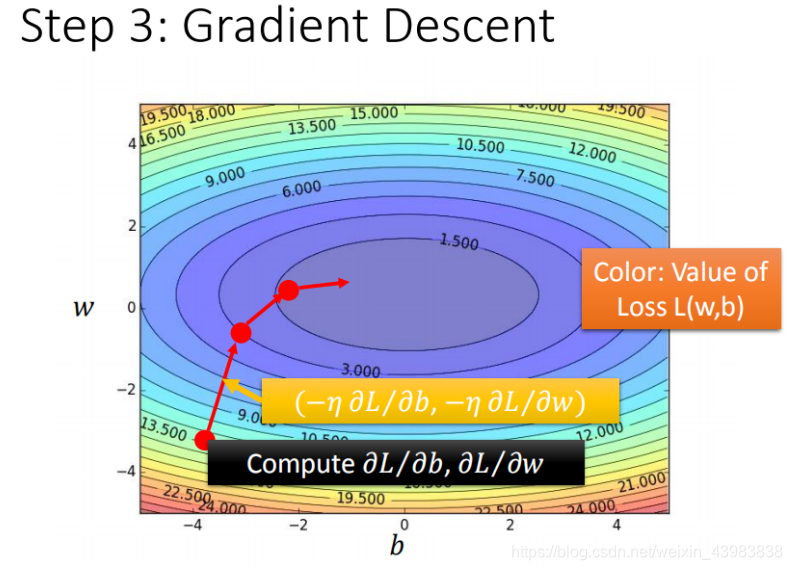
下图对梯度下降的参数更新过程与损失函数的值更新更直观。
补充一个小知识点:
TensorFlow提供了一种灵活的学习率设置方法——指数衰减法
3. 过拟合和正则化
3.1 过拟合
我们可以用 x x x不同阶的模型对点进行拟合。
- 模型越复杂, x x x的阶越高,对training data的拟合效果越好,平均误差越低。
- 但是随着模型对training data的拟合,testing data上的效果反而越差。
这便是出现了过拟合的现象。
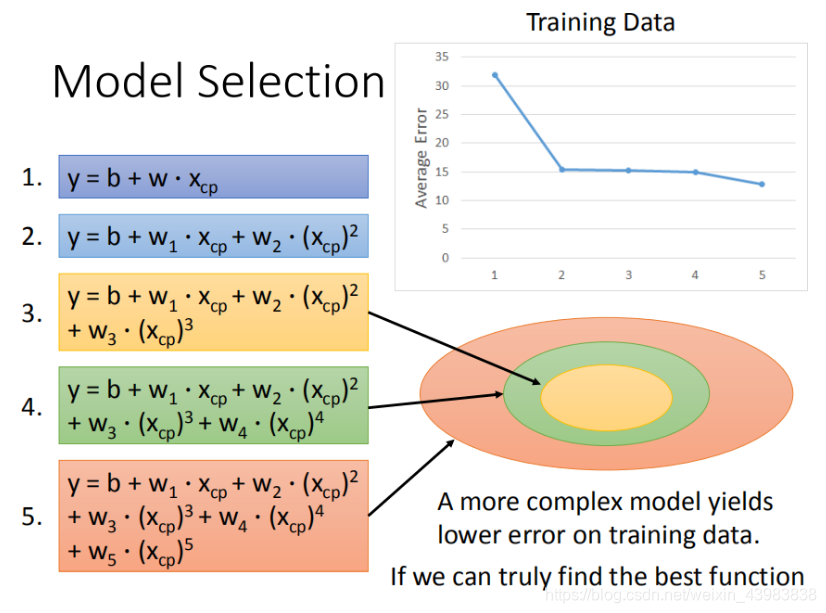

3.2 正则化
权重 w w w可能会使某些特征权值过高,因此我们引入正则化项(来降低 w w w的权重)
- 在使用正则化项时,不需要考虑bais,即 b b b项
- 正则化项使function更平滑






 本文介绍了李宏毅机器学习课程中的线性回归,包括损失函数、梯度下降和过拟合与正则化。讨论了线性回归模型参数、最小二乘法求解最优解,并解释了梯度下降法如何找到全局最优参数。最后,探讨了过拟合现象及正则化项的作用。
本文介绍了李宏毅机器学习课程中的线性回归,包括损失函数、梯度下降和过拟合与正则化。讨论了线性回归模型参数、最小二乘法求解最优解,并解释了梯度下降法如何找到全局最优参数。最后,探讨了过拟合现象及正则化项的作用。

















 2313
2313

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










