【2022省选模拟】星际航道——网格图最小生成树、LCT

没有原题链接

题目描述

题解

如果仅仅是动态维护最小生成树的话，那根本没法在线做。但是这题不一样，突破口就在“网格图”上。

原图是每条边连接两个格点，求格点的最小生成树。假设连接格点的不是一棵树，那么一定出现了>1个格点连通块。我们发现每个格点连通块都是被一圈的正方形空白格子（或者边界）包围，而原本断开这一圈格子和边界的那些边一定不是被选的边。如果我们把每个格子也看成一个节点（特别地，四面的边界全部看成一个节点），规定未选的边连接相邻两个格子节点，那么格子节点一定会形成环。

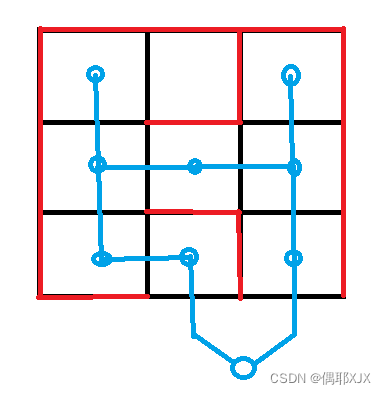
（注：红色是选择的边，蓝色点是格子节点）
再反过来考虑，若格子节点形成了环，那么中间一定有格点被围住，与外界割开，这也就不合法。

所以我们证明，一个连通的格点生成图对应一个格子节点的生成森林，于是一个格点生成树对应一个格子的生成树，一个格点最小生成树就对应着一个格子的最大生成树。（听起来和最大流-最小割一类的问题好像，不会是个线规吧）

于是我们把原问题转化为了一个最大生成树问题😊…可是这不还是一样的不可做吗？

注意到每条边要么在最小生成树中，要么在最大生成树中。在最小生成树问题中，若我们动态修改的边权只会变小，不论修改的边是否在原来的最小生成树上，都是可以用LCT维护的。具体而言只需要挑出路径上的最长边，比较一下，然后插入更优的边即可。类似地，在最大生成树问题中，条件变为了边权只能变大。

把两者结合在一起，不就可以应对所有情况了？

你只需要分类讨论边权是增大还是减小，假设是减小并且不在最小生成树上，那么找最小生成树路径上的最长边，把那条最长边挪到最大生成树上，再把当前修改的边从最大生成树挪到最小生成树上。反过来的情况类似处理。

在线算法，总复杂度 $O(n\log n)$。

代码

#include<bits/stdc++.h>//JZM yyds!!
#define ll long long
#define uns unsigned
#define END putchar('\n')
#define fi first
#define se second
#define IF (it->fi)
#define IS (it->se)
#define lowbit(x) ((x)&-(x))
using namespace std;
const int MAXN=800005;
inline ll read(){
   
   
	ll x=0;bool f=1;char s=getchar();
	while((s<'0'||s>'9')&&s>0){
   
   if(s=='-')f^=1;s=getchar();}
	while(s>='0'&&s<='9')x=(x<<1)+(x<<3)+(s^48),s=getchar();
	return f?x:-x;
}
int ptf[50],lpt;
inline void print(ll x,char c='\n'){
   
   
	if(x<0)putchar('-'),x=-x;
	ptf[lpt=1]=x%10;
	while(x>9)x/=10,ptf[++lpt]=x%10;
	while(lpt)putchar(ptf[lpt--]^48);
	if(c>0)putchar(c);
}

#define pii pair<int,int>
int R,C,A,B,n,m,k;
pii ea[MAXN],eb[MAXN];
ll val[MAXN],sum;
bool on[MAXN];
const ll MX=2e9;
inline void decode(char ch, int &x, int &y, int &w, ll lstans) {
   
   
	static int mask = 0xfffff;
	w = (int) ((w ^ lstans) & mask);
	if(ch == '-') x = (x + lstans - 1) % R + 1, y = (y + lstans - 1) % (C - 1) + 1;
	if