基于pytorch的CNN算法的实现

基于pytorch的CNN算法的实现
2.1.2卷积层：
卷积层的运算方式：
一种对图像的二次转化，使用filter，并提取feature（特征）。

图片1 计算机图片

图片2 像素型图片
计算机图像，所展示的图像为图片1所示但是机器所真正看到只是各个像素点位置的值，平常图像为RGB格式即为三通道，每个通道R(Red)，G(Green)，B(Blue)，并且每个通道上的像素点都有对应的值0-255（可理解为权值），三通道混合后可展现彩色。由于本课题采用图像为灰度图如图片2：1X28X28（单通道28X28像素的灰度图）值为0-1。

图片3卷积核
计算机利用卷积运算：利用图片3：kernal size = 5X5进行运算每个从图片2中抽出5X5的像素进行运算,运算完后再向右一列，一行完后再进行下一行.

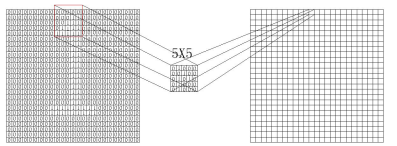
图片4 卷积运算


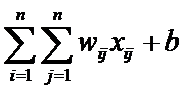
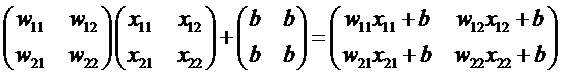
过程即对应相乘：
卷积每一步都会执行这样的以kernal size = 5，stride=1运算最后再一次得到1X23X23，相比以前28X28少了5行5列的信息。
那么其中会用到补0为了尽可能的保留图片信息，padding = 2在图片最外圈补2行2列0值，那么卷积运算在每一行就多运算了5次，则输出的图像又变为1X28X28的图像。
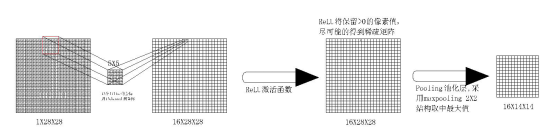
2.1.3激活层：
神经网络的数学基础是处处可微的，所以选取的激活函数要能保证数据输入与输出也是可微的，运算特征是不断进行循环计算，所以在每代循环过程中，每个神经元的值也是在不断变化的。 对于图像，我们主要采用了卷积的方式来处理，也就是对每个像素点赋予一个权值，这个操作显然就是线性的。
但是对于我们样本来说，不一定是线性可分的，为了解决这个问题，我们可以进行线性变化，或者我们引入非线性因素，解决线性模型所不能解决的问题。
所以在课题中使用ReLU激活函数，构建稀疏矩阵，也就是稀疏性，这个特性可以去除数据中的冗余，最大可能保留数据的特征，也就是大多数为0的稀疏矩阵来表示。其实这个特性主要是对于Relu，它就是取的max(0,x)，因为神经网络是不断反复计算，实际上变成了它在尝试不断试探如何用一个大多数为0的矩阵来尝试表达数据特征，结果因为稀疏特性的存在，反而这种方法变得运算得又快效果又好了。目前大部分的卷积神经网络中，基本上都是采用了ReLU 函数。
2.1.4池化层：
其实也是采样层，提取关键特征，并用来降低特征的维度且保留有效信息，一定程度上避免过拟合，还可以减少参数过多导致运算量过大等问题。
池化操作一般有两种，一种是Avy Pooling,一种是max Pooling。
即从中取出2X2的方格后进行平均化再给予下一层，那么图像就会进行压缩为原来的1/4。
即从中取出2X2的方格后取其中最大值再给予下一层，那么图像就会进行压缩为原来的1/4。
2.1.5优化器：
最基础是反向传递：

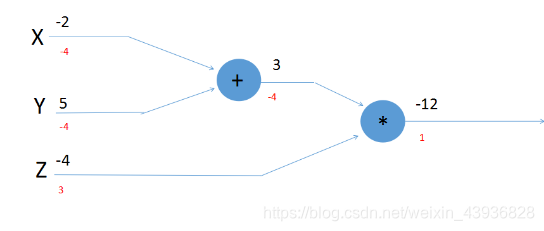
前向传递的过程比较容易理解，进行，即可得出最终结果。
反向传递其实是链式法则：X，Y，Z为输入量中间层为P结果层为F
则：（反向传递的基础过程）

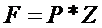
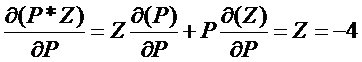
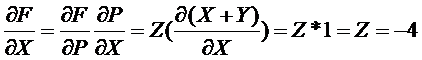
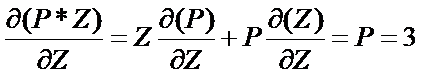
利用上述方法最后加入（最小二乘法）可以概括为反向传递基本方法。
利用损失函数（Target与prediction之间的差值）
利用这些加上Learning Rate（α值）和Loss值的不断减小 可以慢慢拟合曲线等等。
采用的方法Adam算法：
Adam算法就是Momentum+RMSProp的结合，添加了惯性量。也就是在反向传递的过程中添加了部分动量使得寻找下降速度中可以找到最快的路径。
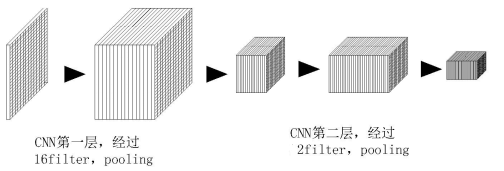
神经网路的架构
数据集：MNIST手写数字数据
第一层的CNN神经网络：
nn.Conv2d(
in_channels = 1,
out_channels = 16
kernel_size = 5,
stride =1,
padding =2,
),
nn.ReLU(),
nn.MaxPool2d(2),
线性分类器：
self.out = nn.Linear(3277,10)
优化器（Adam）：
optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)
loss = nn.CrossEntropyLoss()
back = loss(output,b_y)
测试数据：
test_output, _ = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, ‘prediction number’)
print(test_y[:10].numpy(), ‘real number’)

import torch
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets,transforms
import torch.nn as nn
from torch.autograd import Variable
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt
import os

#Hyper parameters
EPOCH = 1 #traning data n times to save
BATCH_SIZE = 50
LR = 0.001
DOWNLOAD_MNIST = False

train_data = torchvision.datasets.MNIST(
    root='./mnist/',
    train=True,                                     # this is training data
    transform=torchvision.transforms.ToTensor(),    # Converts a PIL.Image or numpy.ndarray to                                            # torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
    download=DOWNLOAD_MNIST,
)

train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)

test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000]/255.   # shape from (2000, 28, 28) to (2000, 1, 28, 28), value in range(0,1)

test_y = test_data.test_labels[:2000]

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(  #1,28,28
            nn.Conv2d(
                in_channels = 1,
                out_channels = 16,#16,28,28
                kernel_size = 5,
                stride =1,
                padding =2,#16,14,14
                #if stride =1 ,padding = (kernel_size-1)/2=()
            ),
            nn.ReLU(),
            nn.MaxPool2d(2),
        )
        self.conv2 = nn.Sequential(         # input shape (16, 14, 14)
                 nn.Conv2d(16, 32, 5, 1, 2),     # output shape (32, 14, 14)
                 nn.ReLU(),                      # activation
                 nn.MaxPool2d(2),                # output shape (32, 7, 7)
                 )
        self.out = nn.Linear(32*7*7,10)   # fully connected layer, output 10 classes if use two layer CNN
        #self.out = nn.Linear(16*14*14,10)   # fully connected layer, output 10 classes if use one layer CNN
    def forward(self,x):
        x = self.conv1(x)
        # x = self.conv2(x)
        x = x.view(x.size(0),-1)
        output = self.out(x)
        return output,x

cnn = CNN()
# print(cnn)
optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)   # optimize all cnn parameters
loss = nn.CrossEntropyLoss()                      # the target label is not one-hotted
# training and testing
for epoch in range(EPOCH):
    for step, (b_x, b_y) in enumerate(train_loader):   # gives batch data, normalize x when iterate train_loader

        output = cnn(b_x)[0]               # cnn output
        back = loss(output, b_y)  # cross entropy loss
        optimizer.zero_grad()           # clear gradients for this training step
        back.backward()                 # backpropagation, compute gradients
        optimizer.step()                # apply gradients
        if step % 50 == 0:
            test_output, last_layer = cnn(test_x)
            pred_y = torch.max(test_output, 1)[1].data.squeeze().numpy()
            accuracy = float((pred_y == test_y.data.numpy()).astype(int).sum()) / float(test_y.size(0))
            print('Epoch: ', epoch, '| train loss: %.4f' % back.data.numpy(), '| test accuracy: %.2f' % accuracy)

test_output, _ = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')

#show the train data no.1 image
# print(train_data.train_data.size())  #60000,28,28
# print(train_data.train_labels.size())
# plt.imshow(train_data.train_data[0].numpy(), cmap = 'gray')
# plt.title('%i' %train_data.train_labels[0])
# plt.show()