神经网络和多层感知机MLP

神经网络和多层感知机MLP

文章内容和代码可由此处查看或下载：

https://github.com/WangXinyuanCSU/DeepLearning-Concepts-and-Implementation

参考：

https://www.cnblogs.com/pinard/p/6422831.html
https://zhuanlan.zhihu.com/p/73214810
https://blog.youkuaiyun.com/tyhj_sf/article/details/79932893

1. 感知机到神经网络，神经网络的基本结构

1.1 感知机

感知机模型是将若干输入加权求和并通过激活函数后输出的模型：

感知机可以表示为线性变换+非线性激活函数：

$z={\sum }_{i=1}^m{w}_i{x}_i+b$

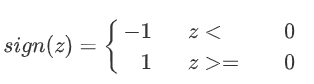
上述模型是一个二分类器，由于其过于简单，无法拟合复杂的非线性任务。

1.2 神经网络及其基本结构

神经网络则是基于这样的简单模型，将多个神经元逐层堆叠，由此形成我们的深度模型：

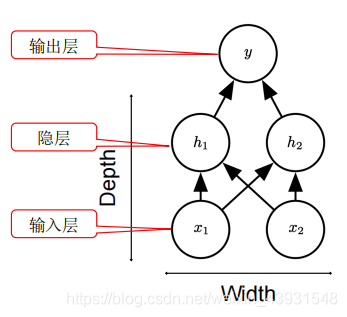
上图是一个最简单的神经网络，它包含神经网络的最基本结构：

​ 输入层：对应输入向量的大小

​ 输出层：对应模型任务，可以是二分类，多分类，也可以是回归任务等等

​ 隐层：由多个感知机，即神经元组成，每个神经元对上层的所有输入做线性变换与非线性激活。

1.3 神经网络参数的定义

​ 神经网络的隐层可以不止一层，宽度也可以很宽，一般来说，我们计算网络层数时不考虑输入层，所以下图是一个４层的神经网络，由于每层神经元连接到上层的所有输入，这个网络也叫做全连接网络，或多层感知机：

​ 由于网络中每层都有参数$w$和$b$，所以我们需要特定的方式进行定义：以下图一个三层的DNN为例，第二层的第4个神经元到第三层的第2个神经元的线性系数定义为$w_{24}^3$。上标3代表线性系数$w$所在的层数，而下标对应的是输出的第三层索引2和输入的第二层索引4。这样定义，每层进行的矩阵运算都可以表示为$w^{T}x+b$。

类似的偏置$b$，第二层的第三个神经元对应的偏倚定义为$b_3^2$。

2. 前向传播

2.1 前向传播原理

上面讲到网络每层从输入到输出都可以表示为线性变换$z=w^{T}x+b$与激活函数$\sigma (z)$，前向传播顾名思义就是从输入层开始，逐层计算输出，最终得到输出层的输出后结束。

​ 例如第二层的输出$a_1^2,a_2^2,a_3^2$，我们有：

$a_1^2=\sigma (z_1^2)=\sigma (w_{11}^2{x}^1+w_{12}^2{x}^2+w_{13}^2{x}^3+b_1^2)$

$a_2^2=\sigma (z_2^2)=\sigma (w_{21}^2{x}^1+w_{22}^2{x}^2+w_{23}^2{x}^3+b_2^2)$

$a_3^2=\sigma (z_3^2)=\sigma (w_{31}^2{x}^1+w_{32}^2{x}^2+w_{33}^2{x}^3+b_3^2)$

​ 对于第三层的的输出$a_1^3$，我们有：

$a_1^3=\sigma (z_1^3$