剑指Offer刷题（五）及思路

二叉树的下一个结点

题目描述
给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

/*
public class TreeLinkNode {
    int val;
    TreeLinkNode left = null;
    TreeLinkNode right = null;
    TreeLinkNode next = null;

    TreeLinkNode(int val) {
        this.val = val;
    }
}
*/
import java.util.*;
public class Solution {
    
    public TreeLinkNode GetNext(TreeLinkNode pNode)
    {
        if(pNode ==null) return null;
        ArrayList<TreeLinkNode> list = new ArrayList<TreeLinkNode>();
        
        TreeLinkNode root =pNode;
        while(root.next!=null)
            root = root.next;
        midSearch(root,list);
        list.add(null);
        for(int i = 0 ;i<list.size();i++)
        {
            if(list.get(i)==pNode)
                return list.get(i+1);
        }
        return null;
    }
    
    void midSearch(TreeLinkNode pNode,ArrayList<TreeLinkNode> list)
    {
        if(pNode==null)return;
        midSearch(pNode.left, list);
        list.add(pNode);
        midSearch(pNode.right, list);
        
    }
}

按中序遍历的顺序把结点存在一个list里即可，再去遍历这个列表，找到要找的结点，然后输出这个结点的下一个

对称的二叉树

题目描述
请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    boolean isSymmetrical(TreeNode pRoot)
    {
        if(pRoot==null)return true;
        return isSym(pRoot.left,pRoot.right);
    }
    
    boolean isSym(TreeNode left,TreeNode right)
    {
    	//左结点为空，右节点为空才对称
        if(left==null) return right==null;
        //左节点不为空，右节点为空则不对称，直接返回false
        if(right==null) return false;
        //左右结点都不为空，值不相同则不对称
        if(left.val!=right.val)return false;
        
        return isSym(left.left,right.right)&&isSym(left.right,right.left);
    }
}

递归地调用，比较子树结构到底即可

按之字形顺序打印二叉树

题目描述
请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

import java.util.*;

/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/

public class Solution {
    public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer> > resList = new ArrayList<>();

        Stack<TreeNode> stack1 = new Stack<TreeNode>();
        Stack<TreeNode> stack2 = new Stack<TreeNode>();

        stack1.push(pRoot);
        while(!stack1.empty()||!stack2.empty())
        {
            ArrayList<Integer> subList = new ArrayList<Integer>();
            while(!stack1.empty())
            {
                TreeNode tmp = stack1.pop();
                if(tmp!=null)
                {
                    stack2.push(tmp.left);
                    stack2.push(tmp.right);
                    subList.add(tmp.val);
                }

            }
            if(!subList.isEmpty())
                resList.add(new ArrayList<Integer>(subList));
            subList.clear();
            while(!stack2.empty())
            {
                
                TreeNode tmp = stack2.pop();
                if(tmp!=null)
                {
                    stack1.push(tmp.right);
                    stack1.push(tmp.left);
                    subList.add(tmp.val);
                }

            }
            if(!subList.isEmpty())
                resList.add(new ArrayList<Integer>(subList));
            subList.clear();
        }
        return resList;
    }

}

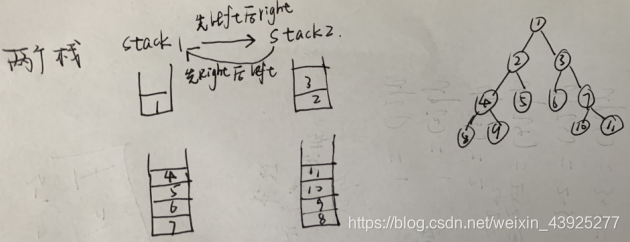
和层次遍历的想法差不多，但是是用两个栈来实现，从stack1弹出结点并往stack2中放该结点的子结点时，先左后右；从从stack2弹出结点并往stack1中放该结点的子结点时，先右后左，出栈顺序依次添加到list中即达成了“之”字形。
注意：往最终结果list中添加成员子list时，要new一个新的并复制，否则如果只是加入子list对象，旧引用对其修改会造成影响

把二叉树打印成多行

题目描述
从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。

import java.util.*;


/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<Integer> subList = new ArrayList<Integer>();
        ArrayList<ArrayList<Integer>> list = new ArrayList<ArrayList<Integer>>();
        LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
        
        if(pRoot==null) return list;
        queue.add(pRoot);
        int nodeNumber = 1;
        int nextNodeNumber = 0;
        while(!queue.isEmpty())
        {
            TreeNode tmp  = queue.remove();
            nodeNumber--;
            subList.add(tmp.val);
            if(tmp.left!=null)
            {
                queue.add(tmp.left);
                nextNodeNumber++;
            }
            if(tmp.right!=null)
            {
                queue.add(tmp.right);
                nextNodeNumber++;
            }
            if(nodeNumber==0)
            {
                list.add(new ArrayList<Integer>(subList));
                nodeNumber = nextNodeNumber;
                subList.clear();
                nextNodeNumber=0;
            }  
        }
        return list;
        
        
    }
    
}

二叉树的层次遍历，要注意返回结果的结构：
ArrayList<ArrayList<Integer>>
要求每一层要分开来，所以需要用两个参数来记录当前层的数量：
nodeNumber，代表当前层的数量，在上一层取队列中元素时做记录;
nextNodeNumber，下一层数量，在当前层取出元素时做记录，最后在下次遍历前赋给当前层，并清零;

序列化二叉树

题目描述
请实现两个函数，分别用来序列化和反序列化二叉树

二叉树的序列化是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串，从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树遍历方式来进行修改，序列化的结果是一个字符串，序列化时通过 某种符号表示空节点（#），以 ！ 表示一个结点值的结束（value!）。

二叉树的反序列化是指：根据某种遍历顺序得到的序列化字符串结果str，重构二叉树。

/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
import java.util.*;

public class Solution {
    //层次遍历
    String Serialize(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        StringBuilder sb = new StringBuilder();
        
        if(root!=null)
        queue.add(root);
        while(!queue.isEmpty())
        {
            TreeNode tmp = queue.poll();
            if(tmp!=null)
            {
                queue.offer(tmp.left);
                queue.offer(tmp.right);
                sb.append(tmp.val+",");
            }
            else{
                sb.append("#"+",");
            }
        }
        if(sb.length()!=0)
        {
            sb.deleteCharAt(sb.length()-1);
        }
        return sb.toString();
       
  }
    TreeNode Deserialize(String str) {
        int length = str.length();
       if(length==0||str==null) return null;
        TreeNode resNode = null;
        
        String[] strArr = str.split(",");
        TreeNode[] nodeArr = new TreeNode[strArr.length];
        for(int i =0 ;i<nodeArr.length;i++)
        {
            if(!strArr[i].equals("#"))
            {
               nodeArr[i] = new TreeNode(Integer.valueOf(strArr[i]));
            }
        }
        int j =1;
        int i =0;
       while(j<nodeArr.length)
       {
           if(nodeArr[i]!=null)
           {
               nodeArr[i].left = nodeArr[j++];
               nodeArr[i].right = nodeArr[j++];
           }
           i++;
       }
        return nodeArr[0];
  }
}

二叉搜索树的第k个结点

题目描述
给定一棵二叉搜索树，请找出其中的第k小的结点。例如， （5，3，7，2，4，6，8） 中，按结点数值大小顺序第三小结点的值为4。

/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
import java.util.*;
public class Solution {

    ArrayList<TreeNode> list = new ArrayList<TreeNode>();
    TreeNode KthNode(TreeNode pRoot, int k)
    {
        if(k==0)return null;
         midSearch(pRoot);
        if(k>list.size())return null;
        return list.get(k-1);
    }
    
      void midSearch(TreeNode root)
    {
        if(root!=null)
        {
            midSearch(root.left);
            list.add(root);
            midSearch(root.right);
        }
    }
    

}

二叉搜索树的中序遍历是排好序的，把其按中序遍历存到一个list中，找到第k-1个即可

滑动窗口的最大值

题目描述
给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

import java.util.*;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size)
    {

        ArrayList<Integer> list = new ArrayList<Integer>();
           if(size==0) return list;
        int length = num.length;
        if(length==0)return list;
        for(int i = 0;i<=length-size;i++)
        {
            int max = num[i];
            for(int j =i;j<size+i;j++)
            {
                if(num[j]>max)max=num[j];
            }
            list.add(max);
        }
        
        return list;
    }
}

矩阵中的路径

题目描述
请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。 例如

​
矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

public class Solution {
    public boolean hasPath(char[] matrix, int rows, int cols, char[] str)
    {
        if(matrix.length==0||matrix==null||str==null||str.length==0)return false;
        boolean[] visited = new boolean[matrix.length];
        for(int i=0;i<rows;i++)
        {
            for(int j=0;j<cols;j++)
            {
                if(walk(matrix,rows,cols,str,i,j,visited,0))
                {
                    return true;
                }
            }
        }
        return false;
    }
    //参数含义： 矩阵数组，行数，列数，要走的字符串路径数组，当前行数，当前列数，标识是否走过的数组，字符串路径数组下标
    boolean walk(char[] matrix, int rows, int cols, char[] str,int i, int j,boolean[] visited,int k)
    {
        //当前位置在 matrix 数组中的下标
        int index = i*cols+j;
        //递归终止条件-失败
        if(i<0||j<0||i>=rows||j>=cols||matrix[index]!=str[k]||visited[index]==true)
            return false;
        //递归终止条件-成功
        if(k==str.length-1)
            return true;
        //递归不终止，则可以走这步
        visited[index] = true;
        
        if( walk(matrix,rows,cols,str,i+1,j,visited,k+1)||
          walk(matrix,rows,cols,str,i,j+1,visited,k+1)||
          walk(matrix,rows,cols,str,i-1,j,visited,k+1)||
          walk(matrix,rows,cols,str,i,j-1,visited,k+1))
        {
            return true;
        }
        //回溯
        visited[index] = false;
        return false;
        
    }
    


}

机器人的运动范围

题目描述
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

public class Solution {

    public int movingCount(int threshold, int rows, int cols)
    {
        int times =0;
        if(rows==0||cols==0)return 0;
        if(threshold==0)return 1;
        boolean[][] matrix = new boolean[rows][cols];
        return move(matrix,rows,cols,0,0,threshold);

    }
    int move(boolean[][] matrix,int rows,int cols,int i,int j,int k)
    {
        //递归结束条件
        if(i<0||j<0||i>=rows||j>=cols||matrix[i][j]==true)
        {
            return 0;
        }
        //若此格子没被访问
        int sum = 0;
        int tmpi = i;
        int tmpj = j;
        while(tmpi>0)
        {
            int tmp = tmpi%10;
            sum +=tmp;
            tmpi /=10;
        }
        while(tmpj>0)
        {
            int tmp = tmpj%10;
            sum +=tmp;
            tmpj /=10;
        }
        if(sum>k)
        {

            return 0;
        }
        matrix[i][j]=true;
       return 1+ move(matrix, rows,cols,i-1, j, k)+
        move(matrix, rows,cols,i+1, j, k)+
        move(matrix, rows,cols,i, j-1, k)+
        move(matrix, rows,cols, i, j+1, k);
    }

}

剪绳子

题目描述
给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1），每段绳子的长度记为k[0],k[1],…,k[m]。请问k[0]xk[1]x…xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。
输入描述:
输入一个数n，意义见题面。（2 <= n <= 60）
示例1
输入
8
输出
18

import java.util.*;
public class Solution {
    public int cutRope(int target) {
        if(target == 0 ||target ==1)return 0;
        int[]dp =new int[target+1];
        dp[2] = 1;
        for(int i=3;i<=target;i++)
        {
            for(int j=1;j<i;j++)
            {
                dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[target];
    }
}

动态规划，
dp[i]代表，长度为i的绳子，剪成多段后最大乘积
j循环代表如果把当前绳子剪成两段，一段A为j，另一段B为i-j
则它们的乘积为j*(i-j)，那么要不要再继续剪另一段B呢？
看j*dp[i-j]，另一段B的最大乘积为dp[i-j]（这个是决定再剪B之后，B的最大乘积），取 不剪B 和剪B 结果的最大的那个即可

剩了 数据流的中位数 和 正则表达式匹配 没有做，共做了65题，许多题并非最优解，这里只作记录参考。