业余笔记·收智商税的题

最新推荐文章于 2025-08-13 21:50:23 发布

原创最新推荐文章于 2025-08-13 21:50:23 发布 · 249 阅读

0 ·

CC 4.0 BY-SA版权

本文探讨了ACM竞赛中非传统算法题目的解决思路，通过实例分析展现了旁门左道的魅力。深入讲解了“救公主”等题目背后的策略，并分享了比赛心态调整的重要性。代码示例展示了如何巧妙处理复杂债务网络，实现高效匹配。

怎么说这类问题呢，感觉终属旁门左道，而且有点背离了算法竞赛的初衷。但确实比赛中会有（2019南京区域赛救公主那道题），而且想到时会有豁然开朗的感觉，这也是ACM迷人的地方之一。
况且，ACM本来就不叫算法设计大赛鸭。。。

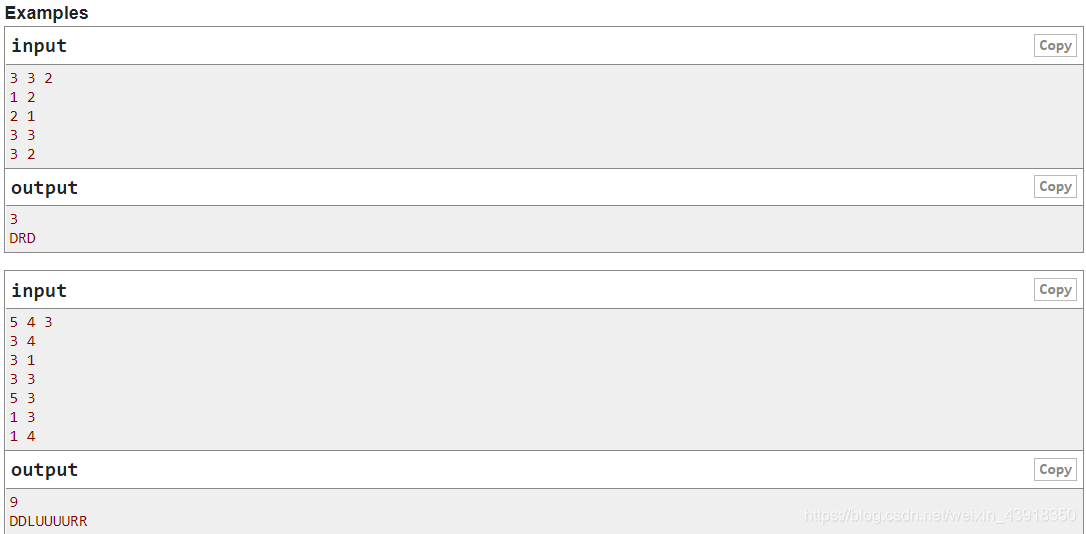
C. Game with Chips

原题地址
在这里插入图片描述

代码：
先把所有点集中到右下角，然后遍历一遍图。
和输入一点毛关系没有你敢信？
一开始读了假题，然后心态一直崩，越做越崩。。。
时隔一年再次div2只A了两题

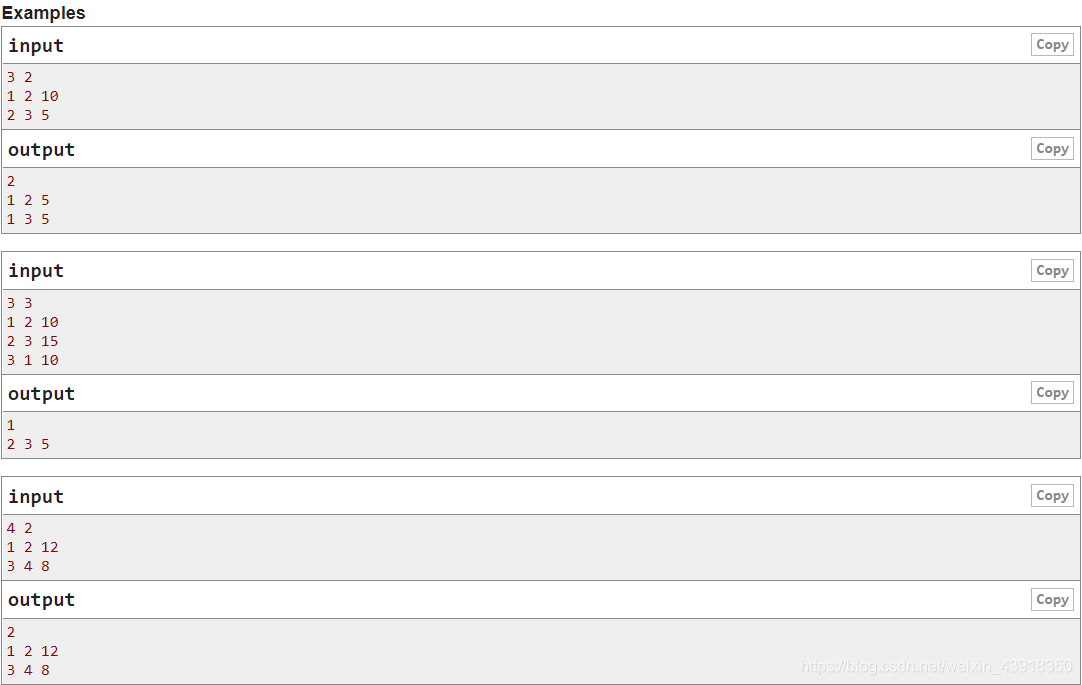
D. Decreasing Debts

原题地址
在这里插入图片描述

代码：
刚看题的时候想了很多算法，网络流、匈牙利。。。
结果看了眼题解。。。题解

#include<iostream>
#include<vector>
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 3e5 + 1000;
typedef long long ll;
ll v[N];
vector<int> in, out, ans1, ans2;
vector<ll> ans3;
int n, m;
int main()
{
	scanf("%d %d", &n, &m);
	while (m--)
	{
		int x, y; ll z;
		cin >> x >> y >> z;
		v[x] += z; //支出
		v[y] -= z;//收入 
	}
	for (int i = 1; i <= n; i++)
	{
		if (v[i] > 0) out.push_back(i); //支出 
		if (v[i] < 0) in.push_back(i);//收入 
	}
	int i = 0, j = 0;
	while (1)
	{
		if (i == out.size() && j == in.size()) break;
		ll value = min(v[out[i]], -v[in[j]]);
		ans1.push_back(out[i]);
		ans2.push_back(in[j]);
		ans3.push_back(value);
		v[out[i]] -= value;
		v[in[j]] += value;
		if (v[out[i]] == 0) i++; //换到下一个人匹配
		if (v[in[j]] == 0) j++;

	}
	cout << ans1.size() << endl;
	for (int i = 0; i < ans1.size(); i++)
	{
		cout << ans1[i] << " " << ans2[i] << " " << ans3[i] << endl;
	}
	return 0;
}