寒假笔记二·解析几何相关

E. New Year and Castle Construction

原题地址


代码：
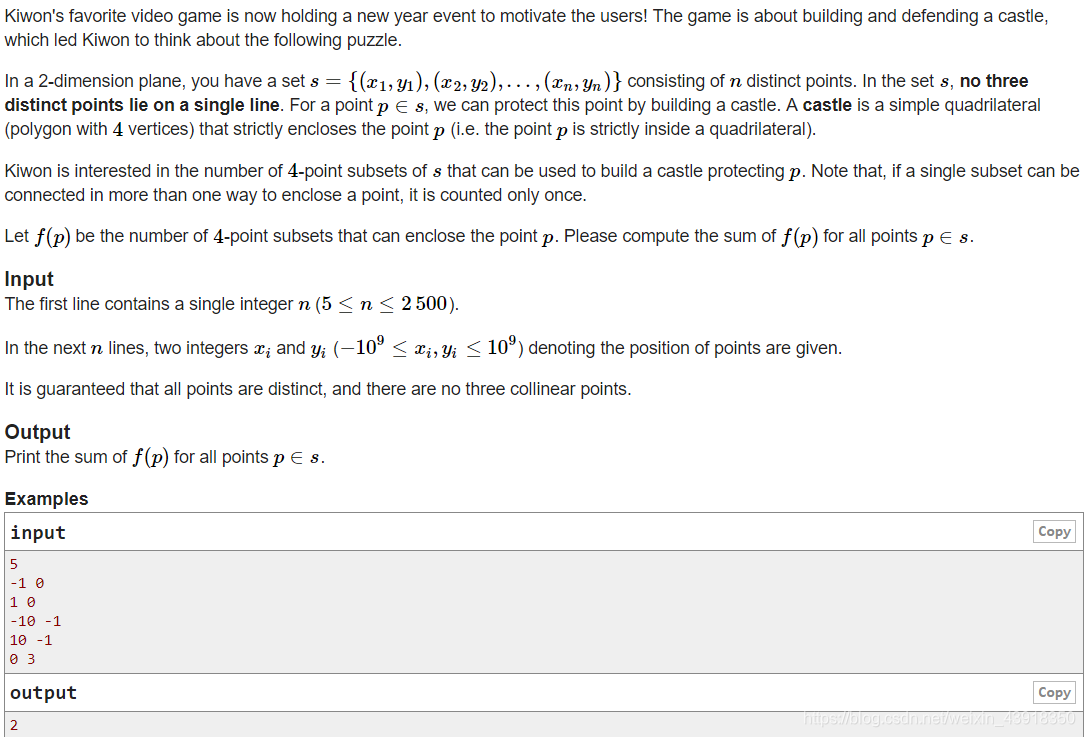
题目大意：平面上有n个点，任意三点不共线，定义一个合法组合为一个中心点，和四个其它点，要求中心点在四个点围成的四边形内部。询问有多少合法组合。
看了一些博客，思路大体相同，先得出所有方案数为n*C(n-1,4)，然后排除不合法方案数。
但对于判定不合法方案数的理解上，感觉略有不同
有第一种理解
个人更倾向于第二种理解
代码写出来倒是一样的。
注意atan2的用法atan2

#include<iostream>
#include<vector>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<map>
using namespace std;
typedef long long ll;
const long double pi = acos(-1.0L);//必须开long double
const int maxn = 2e3+600;
long double x[maxn],y[maxn];
int main()
{
    int n;cin>>n;
    ll ans = (ll)n*(n-1)*(n-2)*(n-3)*(n-4)/24; 
    for(int i = 0;i<n;i++)
	{
        ll xi,yi;
        cin>>xi>>yi;
        x[i] = xi,y[i] = yi;
    }
    for(int i = 0;i<n;i++)
	{
        vector<long double> v;
        for(int j = 0;j<n;j++)
		{
            if(i == j) continue;
            v.push_back(atan2(y[j]-y[i],x[j]-x[i])); //算一下角度 
        }
        sort(v.begin(),v.end());//做极角排序 
        int k = n - 1 , cur = 0;
        for(int j = 0;j<k;j++)//这里我理解为从第j个点开始转
		{
            while(cur < j+k)//类似滚尺法
			{ 
                long double angle = v[cur%k] - v[j];//枚举两条边的夹角 
                if(angle < 0) angle+=2*pi;//如果角度小于0,则增加2*pi转一圈 
                if(angle < pi) cur++;//如果该点在枚举的这条线上面，则cur++ 
                else break;
            }
            long long cnt = cur - j - 1;
			//想象一个钟，i点为圆心，cur为走在前面的指针
			//j点为走在后面的指针，保持两指针夹角小于pi
			//cnt为两指针间的点数
            ans-=1ll*cnt*(cnt-1)*(cnt-2)/6;
        }
    }
    cout<<ans<<endl;
    return 0;
}