删除一次得到子数组最大和（动态规划）_java删除一次得到子数组最大和-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43900761/article/details/101038986

子数组最大和

题目
题解

题目

力扣删除一次得到子数组最大和（动态规划）

给你一个整数数组，返回它的某个非空子数组（连续元素）在执行一次可选的删除操作后，所能得到的最大元素总和。

换句话说，你可以从原数组中选出一个子数组，并可以决定要不要从中删除一个元素（只能删一次哦），（删除后）子数组中至少应当有一个元素，然后该子数组（剩下）的元素总和是所有子数组之中最大的。

注意，删除一个元素后，子数组不能为空。

示例 1：
输入：arr = [1,-2,0,3]
输出：4
解释：我们可以选出 [1, -2, 0, 3]，然后删掉 -2，这样得到 [1, 0, 3]，和最大。

示例 2：
输入：arr = [1,-2,-2,3]
输出：3
解释：我们直接选出 [3]，这就是最大和。

示例 3：
输入：arr = [-1,-1,-1,-1]
输出：-1
解释：最后得到的子数组不能为空，所以我们不能选择 [-1] 并从中删去 -1 来得到 0。
我们应该直接选择 [-1]，或者选择 [-1, -1] 再从中删去一个 -1。

题解

连续子数组的最大和

要解上面那道题，首先要先会写这道题：
连续子数组的最大和

输入一个非空整型数组，数组里的数可能为正，也可能为负。
数组中一个或连续的多个整数组成一个子数组。
求所有子数组的和的最大值。
要求时间复杂度为O(n)。

样例
输入：[1, -2, 3, 10, -4, 7, 2, -5]
输出：18

其实这是一道很简单的动态规划题目
就不在这里讲解法了，不懂的可以看看下面2篇博客
思路和 Java代码
 C代码

本题思路

本题说明可以删除一个数字，即找出这个数组中的某一数字x，用 x左边剩余数组的最大值 + x右边剩余数组的最大值用动态规划存储在一个新数组中，从而找出此数组中的最大值。

例如：
求这个数组删除一数后的最大子数组：

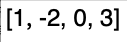
从第2位数开始遍历（即 x 为 -2 ）：

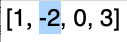
按照上面的思路，就会得到这样的结果：

而通过求连续子数组的最大和，即可求到
左边数组[1]的最大值为 1 ;
右边[0, 3]的最大值为 3 ;
所以在删除 -2 后，此数组的最大值为 1 + 3 = 4。
然后继续遍历。

思路分析代码

1. 先求出每一位的左右子数组最大和

（1）左边子数组最大和

    for(i = 1; i < n; i++) {
      left[i] = max(dp1[i - 1] + a[i], a[i]); 
    }

（2）右边子数组最大和

    for(i = n - 2;i >= 0; i--) {
      right[i] = max(dp1[i + 1] + a[i], a[i]); 
    }

注意：因为可能存在不删除数字就得到最大和的情况，所以要求出 left[ ] 数组和 right[ ] 数组中的最大值，用max_right_left记录。

2. 用动态规划，求出在删除数字 i 后的子数组最大值，存入新数组中

    dp[0] = left[0] + right[2]
    for(i = 1;i < n - 1; i++) {
      //dp[i] = max(left[i - 1] + right[i + 1], dp[i - 1]); 
      dp[i] = left[i - 1] + right[i + 1];
    }