【LeetCode】982. 按位与为零的三元组

982. 按位与为零的三元组

题目描述

给你一个整数数组 nums ，返回其中 按位与三元组 的数目。

按位与三元组 是由下标 (i, j, k) 组成的三元组，并满足下述全部条件：

• 0 <= i < nums.length
• 0 <= j < nums.length
• 0 <= k < nums.length
• nums[i] & nums[j] & nums[k] == 0 ，其中 & 表示按位与运算符。

---

示例 1

输入：nums = [2,1,3]
输出：12
解释：可以选出如下 i, j, k 三元组：
(i=0, j=0, k=1) : 2 & 2 & 1
(i=0, j=1, k=0) : 2 & 1 & 2
(i=0, j=1, k=1) : 2 & 1 & 1
(i=0, j=1, k=2) : 2 & 1 & 3
(i=0, j=2, k=1) : 2 & 3 & 1
(i=1, j=0, k=0) : 1 & 2 & 2
(i=1, j=0, k=1) : 1 & 2 & 1
(i=1, j=0, k=2) : 1 & 2 & 3
(i=1, j=1, k=0) : 1 & 1 & 2
(i=1, j=2, k=0) : 1 & 3 & 2
(i=2, j=0, k=1) : 3 & 2 & 1
(i=2, j=1, k=0) : 3 & 1 & 2

---

示例 2

输入：nums = [0,0,0]
输出：27

---

提示

• 1 <= nums.length <= 1000
• 0 <= nums[i] < 2¹⁶

---

算法一：哈希表 + 枚举

思路

• 首先遍历 nums 的前两个值，因为题目中提到 0 <= nums[i] < 2¹⁶ ，所以我们可以把这两个值按位与的结果存放到哈希表的索引，哈希表的值为按位与结果的出现次数，这样的时间复杂度为 O（n² + 2¹⁶ * n） 。

收获

• 我一开始的想法是：先计算前两个的值，存入数组中，然后再遍历数组的值与第三个 num ，但其实这样也是 三重循环，复杂度也是 O（n³） ，显然超时了；因此看了题解，复杂度可以降到 O（n² + 2¹⁶ * n）。

算法情况

• 时间复杂度： O（n² + 2¹⁶ * n），其中 n 为 nums.size();

• 空间复杂度：O（2 ¹⁶）；

  

代码

class Solution {
public:
    int countTriplets(vector<int>& nums) {
        int ans = 0;
        vector<int> cnt(1<<16);
        for(int x : nums){
            for(int y : nums){
                cnt[x & y] ++;
            }
        }
        for(int n : nums){
            for(int i=0; i<(1<<16); ++i){
                if((i & n) == 0) ans += cnt[i];
            }
        }
        return ans;
    }
};

算法二：哈希表 + 枚举优化

思路

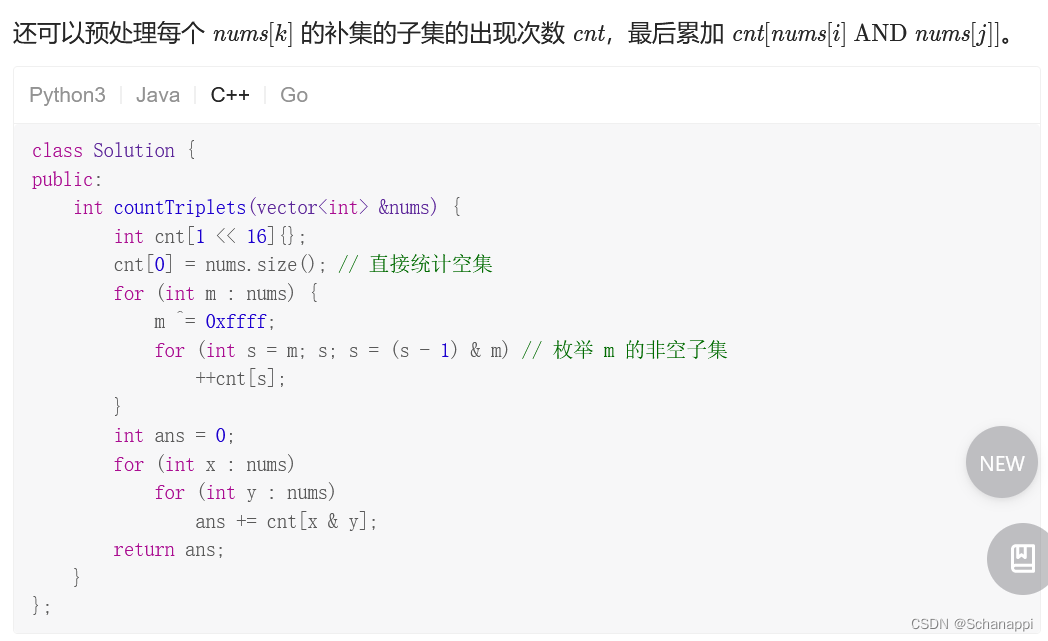
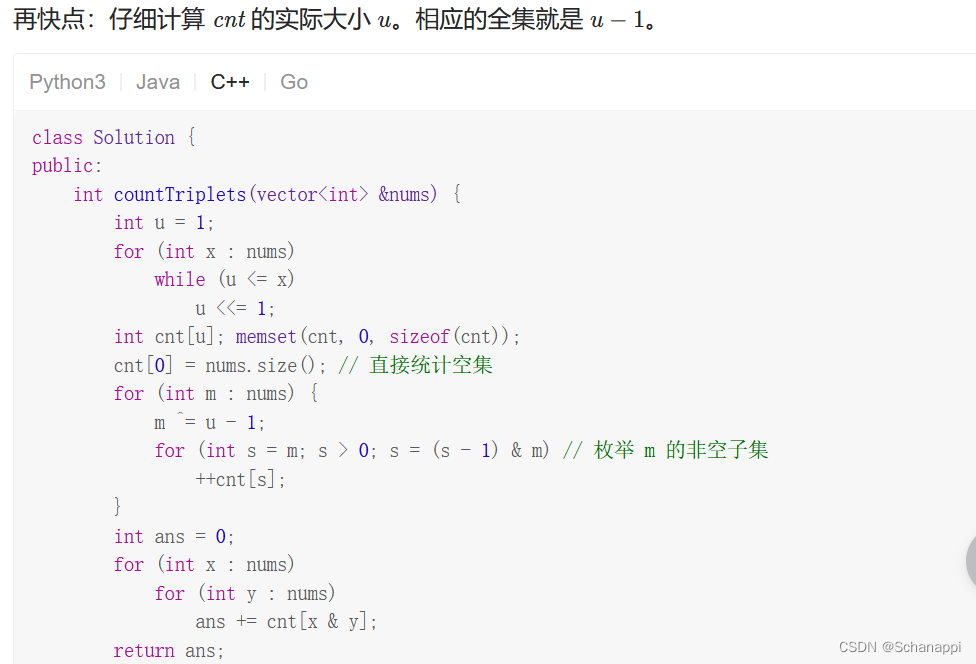
算法情况

• 时间复杂度： O(n(n+U))，其中 n 为 nums 的长度，U=max⁡(nums)；

• 空间复杂度：O(U) 。

  

代码

class Solution {
public:
    int countTriplets(vector<int>& nums) {
        int ans = 0;
        int u=1;
        // 预先计算数组 cnt 的实际大小
        for(int n : nums){
            while(u <= n){
                u <<= 1;
            }
        } 
        vector<int> cnt(u);

        cnt[0] = nums.size();

        for(int n : nums){
            int m = (u-1) ^ n;
            for(int s=m; s; s=(s-1)&m){
                cnt[s]++;
            }
        }
        for(int x : nums){
            for(int y : nums){
                ans += cnt[x & y];
            }
        }
        return ans;
    }
};

参考资料

1. 有技巧的枚举 + 常数优化（Python/Java/C++/Go）