实验十装载问题

最新推荐文章于 2021-12-15 23:28:28 发布

想和李白喝酒

最新推荐文章于 2021-12-15 23:28:28 发布

阅读量318

点赞数

分类专栏：作业文章标签：算法

本文链接：https://blog.youkuaiyun.com/weixin_43894437/article/details/117219539

版权

作业专栏收录该内容

13 篇文章

订阅专栏

一.问题

n个集装箱装上两艘载重分别为C和C2的轮船，w为集装箱i的重量，且之，W≤q+c2
问是否存在一种合理的装载方案将n个集装箱装上轮船?如果有，给出一种方案。

二.解析

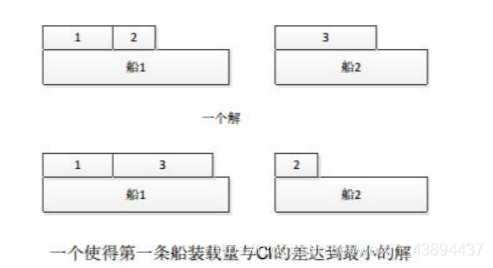
定理:如果装载问题有解，则存在一一个使得第一条船装载量与c1的差达到最小的解。
证明:如果有解，假设一个解为船1 (c1)上装载: w1和w2
船2 (c2)上装载: w3，并且c1-(w1+w2)不为最小解。
由于现有解c1 -(w1+w2)不为最小解，则通过交换c1和c2上的物品，使得存在更小解，例如交换w2和w3，使得c1-(w,+W)<c1-(w1+w2);
通过以上方法，直到找到一个使得第一条船装载量与c1的差达到最小的解。
在这里插入图片描述

三.设计

(1)将w1, w2… wn按照递降排序(降序的目的是加快回溯，大的数据容易超出船1的载重).
(2)解向量<x1,x2…xk>. 其中x∈{0,1},1≤i≤n搜索空间是子集树
(3)在结点<x1,x2...xk >的约束条件:ΣWiXi≤c1(k,i=1)(4)满足多米诺条件: P.x.....++，(:.x2.....+)的某个性质P(x,2....Xk+1)→P(x2.....xk) (0<k<n)要使回溯算法得到正确应用，必须满足多米诺性质.
在这里插入图片描述