简介
pytorch优化器:管理并更新模型中可学习参数的值,是的模型输出更接近真实标签。
导数:函数在指定坐标轴上的变化率
方向导数:指定方向上的变化率
梯度:一个向量,方向为方向导数取得最大值的方向
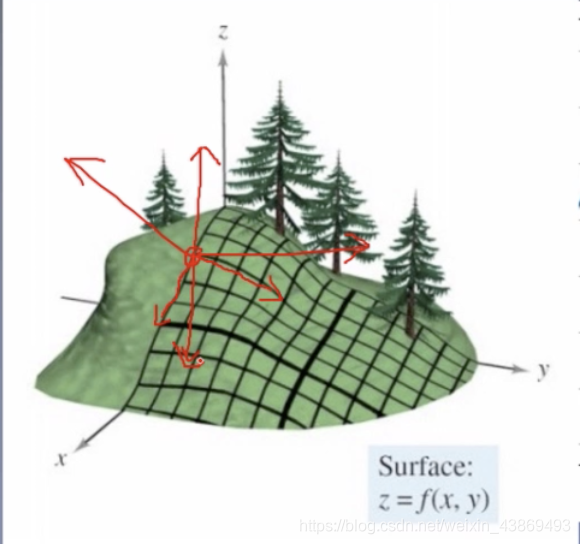
pytorch中的optimizer
基本属性:
- default:优化器超参数
- state:参数的缓存,如momentum的缓存
- param_groups:管理的参数组
- _step_count:记录更新次数,学习率调整中使用

基本方法
- zero_grad():清空所管理参数的梯度
pytorch特性:张量梯度不会自动清零 需要在使用完梯度之后需要清零 - step():实行一步参数更新
- add_param_group():添加参数组
- state_dict():获取优化器当前状态信息字典
- load_state_dict():加载状态信息字典
后两个方法,用于模型断点状态训练
optimizer=optim.SGD(net.parameters(),lr=LR,momentum=0,9) #选择优化器
scheduler=torch.optim.lr_scheduler.StepLR(optimizer,step_size=10,gamma=0.1) #设施学习率下降策略
保存优化器信息
torch.save(optimizer.state_dict(),os.path.join(BASE_DIR,"optimizer_state_dict.pkl"))
##lode sate_dict
state=torch.load(os.path.join(BASE_DR,"optimizer_state_dict.pkl"))
optimizer.load_sate_dict(state)
学习率
梯度下降:Wi+1=Wi−g(Wi)W_{i+1}=W_{i}-g(W_{i})Wi+1=Wi−g(Wi)
y=f(x)=4∗x2y′=f′(x)=8∗xy=f(x)=4*x^2 \\
y'=f'(x)=8*xy=f(x)=4∗x2y′=f′(x)=8∗x
x0=2,y0=16,f′(x0)=16x1=x0−f′(x0)=2−16=−14x1=−14,y1=784,f′(x1)=−112x2=x1−f′(x1)=−14+112=98,y2=38416....x_{0}=2,y_0=16,f'(x_0)=16 \\ x_1=x_0-f'(x_0)=2-16=-14 \\ x_1=-14,y_1=784,f'(x_1)=-112 \\ x_2=x_1-f'(x_1)=-14+112=98,y_2=38416 ....x0=2,y0=16,f′(x0)=16x1=x0−f′(x0)=2−16=−14x1=−14,y1=784,f′(x1)=−112x2=x1−f′(x1)=−14+112=98,y2=38416....
可以看出,如果没有学习率,损失值并不会收敛,很容易梯度爆炸
修正之后的公式:Ww+1=Wi−LR∗g(Wi)W_{w+1}=W_{i}-LR*g(W_i)Ww+1=Wi−LR∗g(Wi)
学习率(learning rate)控更新的步伐
动量(Momentum)
Momentum(动量、冲量):结合当前梯度与上一次更新信息,用于当前更新
指数加权平均:vt=vt−1+(1−β)∗θt指数加权平均:v_t=v_{t-1}+(1-\beta)*\theta_t指数加权平均:vt=vt−1+(1−β)∗θt
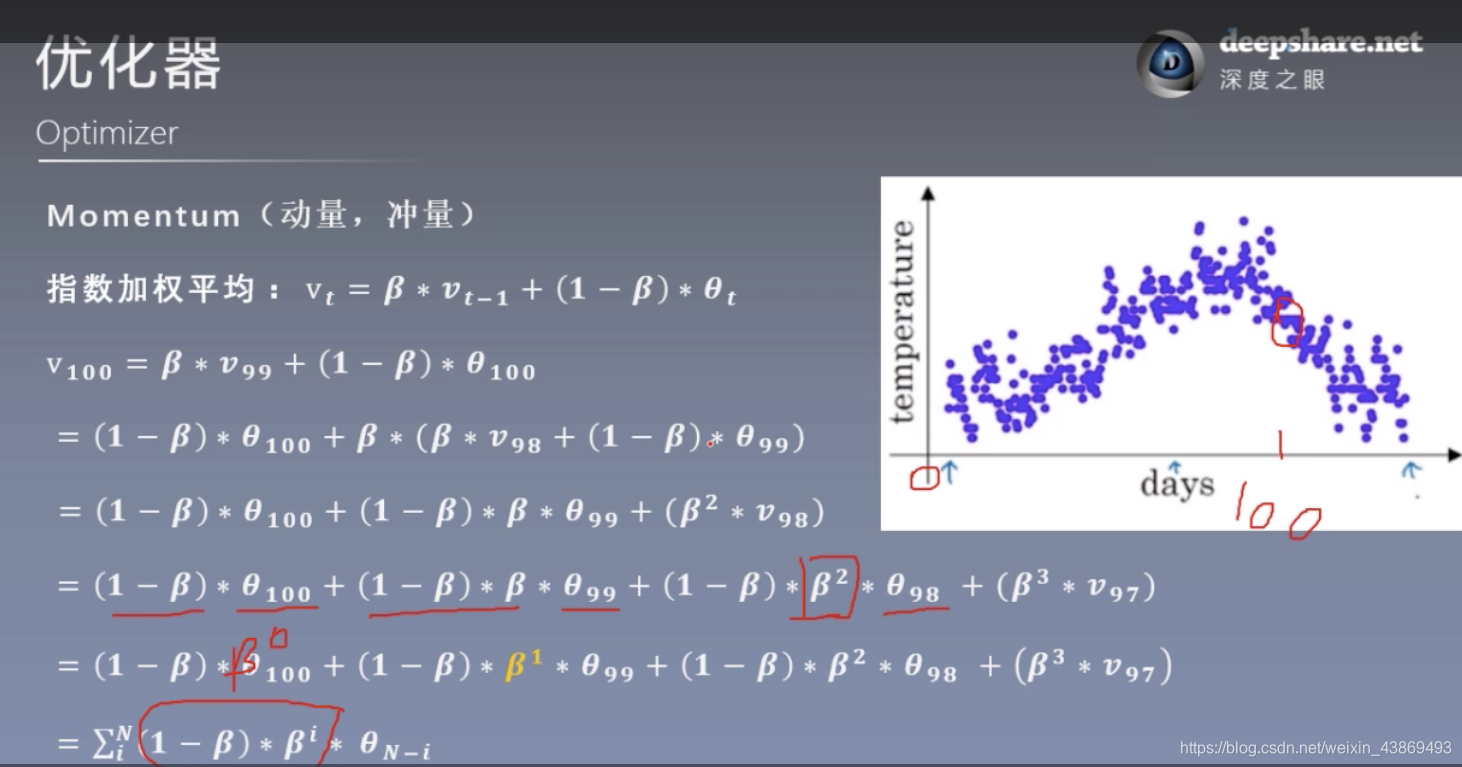
个人看法:可以看到这个式子认为,100这个点对应的更新量是和之前的所有点的值有关,只不过里100这个点越近的点,权值越大,有点类似于自控原理里面的主导极点
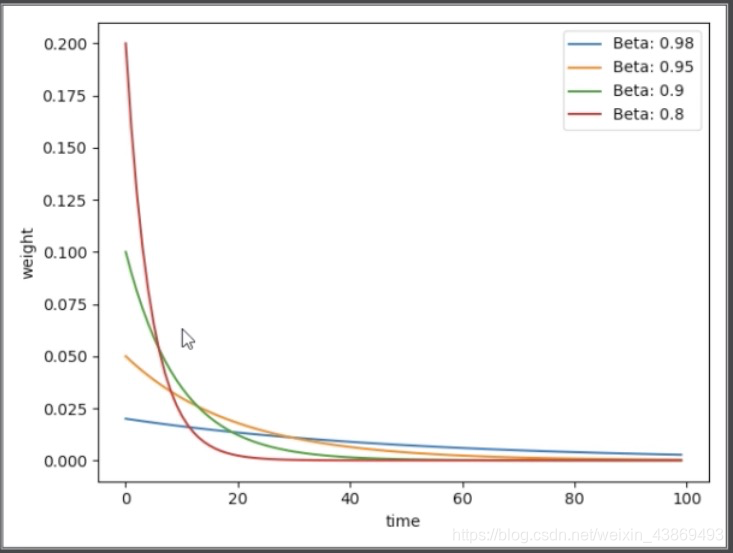
动量值通常取0.9
常用的优化器
1.optim.SGD


2.推荐使用SGD和Adam





















 3777
3777

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








