DPL中的权植initiation方法

参数初始化的基本条件

什么样的初始化参数才是最好的呢？这里直接引入几个参数初始化的要求：
在Xavier论文中，作者给出的Glorot条件是：正向传播时，激活值的方差保持不变；反向传播时，关于状态值的梯度的方差保持不变。这在本文中稍作变换：正向传播时，状态值的方差保持不变；反向传播时，关于激活值的梯度的方差保持不变。
Glorot条件：优秀的初始化应该保证以下两个条件：

1）各个层的激活值h（输出值）的方差要保持一致，即

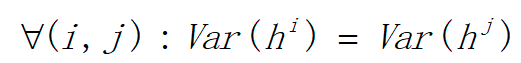
2）各个层对状态Z的梯度的方差要保持一致

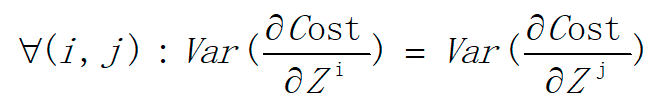
因此， Xavier & kaiming 初始化做了以下工作。

Xavier Initialization：

https://prateekvjoshi.com/2016/03/29/understanding-xavier-initialization-in-deep-neural-networks/
https://www.cnblogs.com/hejunlin1992/p/8723816.html
我们假设所有的输入数据x满足均值为0，方差为$${\delta }_x$$的分布，我们再将参数w以均值为0，方差为$${\delta }_w$$的方式进行初始化。我们假设第一层是卷积层，卷积层共有n个参数（n=channelkernel_hkernel_w），于是为了计算出一个线性部分的结果，我们有：

$$Z_j=\sum _{i=1}^n{x}^i{w}^i$$

其中，忽略偏置b。

假设输入x和权重w独立同分布，我们可以得出z服从均值为0，方差为：
$$Var(Z)=n\ast {\delta }_x\ast {\delta }_w$$
如果输入输出要保持同一分布则要使：

才能保证：
$$Var(Z_i)=Var(Z_{i+1})$$

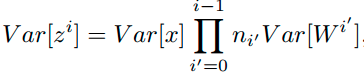
特别的，反向传播计算梯度时同样具有类似的形式：

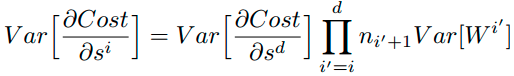
综上，为了保证前向传播和反向传播时每一层的方差一致，应满足：

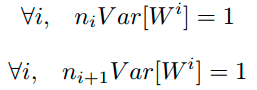
但是，实际当中输入与输出的个数往往不相等，于是为了均衡考量，最终我们的权重方差应满足：
学过概率统计的都知道 [-a,a] 间的均匀分布的方差为：

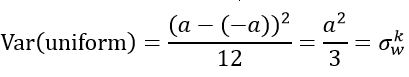
因此，Xavier初始化的实现就是下面的均匀分布：

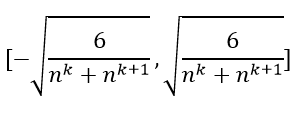
Xavier的均匀分布：
$$tensor\to U[-a,a],其中：a=\sqrt{\frac{6}{fan\_in+fan\_out}}$$
也可以推导出Xiver的正态分布：

$$tensor\to \delta [0,std],其中：std=\sqrt{\frac{2}{fan\_in+fan\_out}}$$

kaiming Initialization:

https://blog.youkuaiyun.com/winycg/article/details/86649832
Xavier在tanh中表现的很好，但在Relu激活函数中表现的很差，所何凯明提出了针对于relu的初始化方法。pytorch默认使用kaiming正态分布初始化卷积层参数。

torch.nn.init.kaiming_uniform_
	(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

kaiming的均匀分布：
$$tensor\to U[-a,a],其中：a=\sqrt{\frac{6}{(1+a^2)\ast fan\_in}}$$
a:激活函数的负斜率
fan_in:默认为fan_in模式，fan_in可以保持前向传播的权重方差的数量级，fan_out可以保持反向传播的权重方差的数量级。

kaiming的正态分布：

torch.nn.init.kaiming_normal_
	(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

$$tensor\to \delta [-0,std],其中：std=\sqrt{\frac{2}{(1+a^2)\ast fan\_in}}$$

扩展阅读：
https://blog.youkuaiyun.com/weixin_41278720/article/details/89819092