【机器学习】01-线性回归学习笔记

最新推荐文章于 2024-07-03 21:56:37 发布

原创

最新推荐文章于 2024-07-03 21:56:37 发布 · 1.1k 阅读

CC 4.0 BY-SA版权

文章标签：

例子：房价预测
属于有监督学习
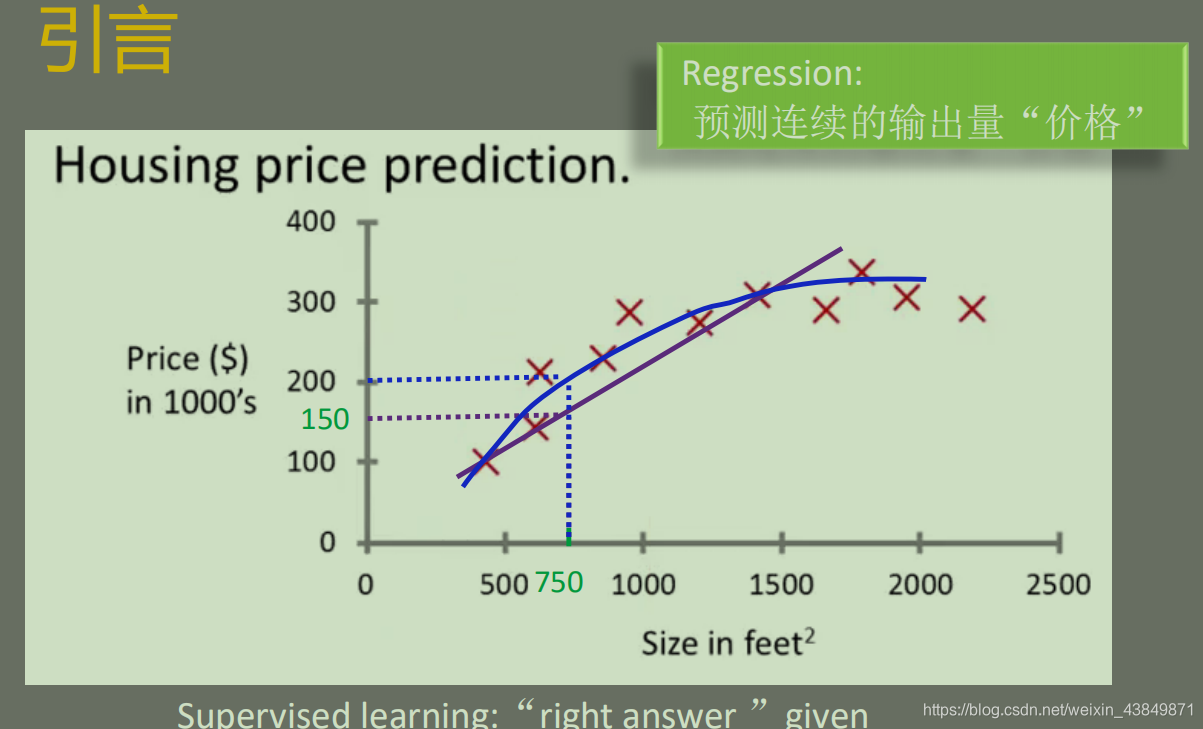
在这里插入图片描述

从给定输入和输出的训练即中学习输入和输出之间的映射函数，然后利用该映射函数预测出测试样本的输出值，其中训练集中的每个样本都由输入和对应的输出（也称之为label）组成（labeld data）
- 回归（Regression）——预测的目标值是数值型，连续变量
- 分类（Classification）——预测的目标值是离散的

1.回归

根据自变量 $x_1,x_2,...,x_n$ 以及因变量y的观测样本，去估计两者之间近似的函数关系 $f$
- 通常，假设函数 $f$ 的数学形式是已知的，但其中的若干个参数未知
- 通过自变量和因变量的观测样本去估计未知的参数值—— $\color{yellow}{参数回归}$

2.线性回归

$y=w_0+w_1x_1+w_2x_2+...+w_nx_n$ ,
其中W=[ $w_0w_1w_2...w_n$ ]为回归系数
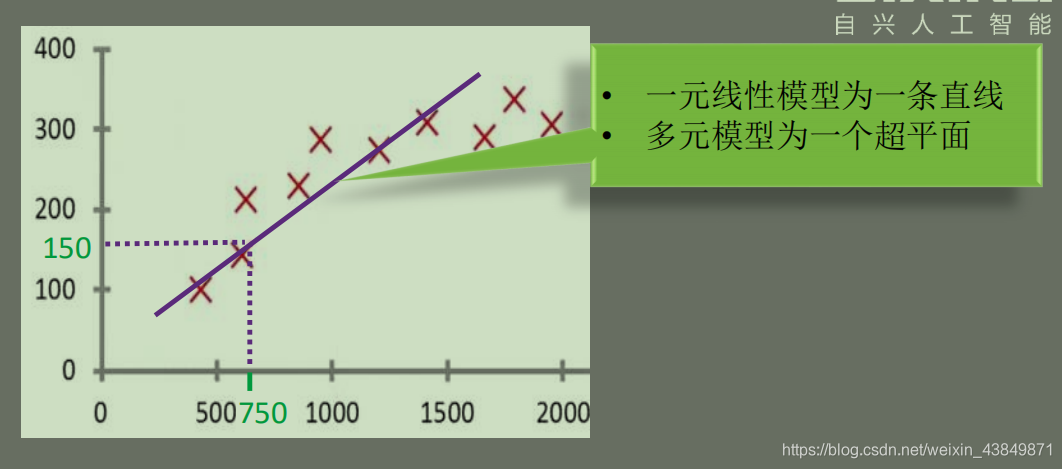
在这里插入图片描述
一元回归

多元回归

回归

例——房价预测

多项式回归可转换为多元线性回归

一元m次多项式回归方程
$y=w_0+w_1x+w_2x^2+...+w_mx^m$
可转换为m元线性回归方程
$y=w_0+w_1x_1+w_2x_2+...+w_mx_m$
其中 $x_i=x^i$
二元二次多项式回归方程
$y=a_0+a_1x_{1}^{2}+a_2x_{2}^{2}+a_3x_{1}x_{2}+a_4x_1+a_5x_2$
可转换为5元线性回归方程
$y=w_0+w_1z_1+w_2z_2+w_3z_3+w_4z_4+w_5z_5$
其中 $z_1=x_{1}^{2}，z_2=x_{2}^{2}，z_3=x_{1}x_{2}，z_4=x_1，z_5=x_2$

收集数据，采集训练样本，每个训练样本包括特征向量及其对应的期望输出

假设有n个已标记的样本数据， $X_i$ 为第i个样本， $y_i$ 是该样本给定的期望输出
- 其中 $X_i=[x_0=1,x_1,x_2,...,x_m]$
- 回归系数W=[w_0,w_1,…,w_m]
- 预测值 $y_i'=X_iW$
$\color{yellow}{设计训练算法找到回归系数}$