【数据结构】串（三）—— KMP 算法

前言

在串的朴素模式匹配算法中，每趟匹配失败都是模式后移一位再从头开始比较。为此本章介绍一种改进的模式匹配算法 —— KMP 算法。

一、两种模式匹配算法的比较

以下面主串的模式匹配为例

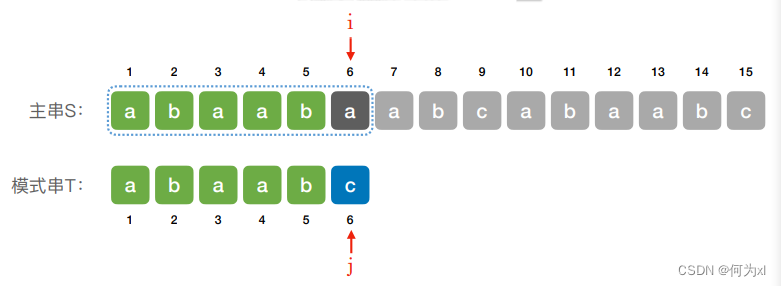
朴素模式匹配算法：

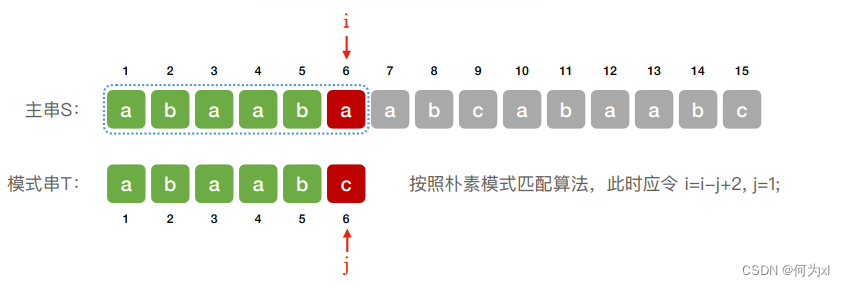
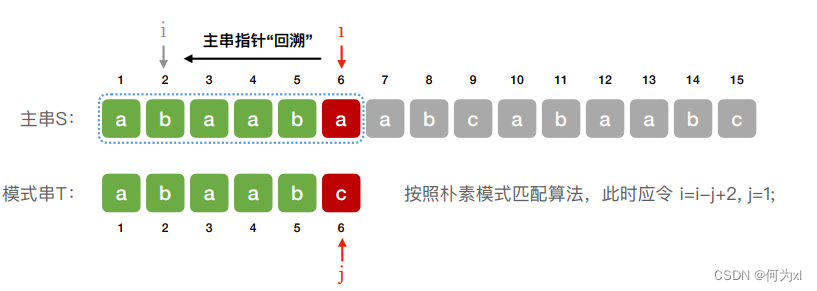
朴素模式匹配，主串有回溯

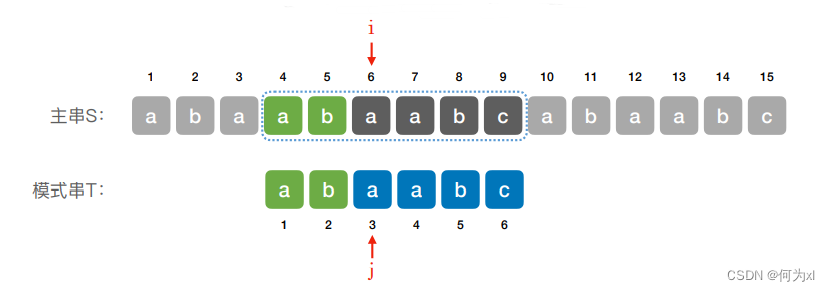
KMP算法：
在保证指针 i 不回溯的前提下，当匹配失败时，让模式串向右移动最大的距离；

二、KMP 算法的实现

KMP算法相较于朴素模式匹配算法的优势在于：在保证指针 i 不回溯的前提下，当匹配失败时，让模式串向右移动最大的距离.

为此计算模式串向右移动的距离是极为重要的，一般使用 next 数组来存储相关距离值。

1. next 数组的计算

（一）、字符串的前缀、后缀和部分匹配值

要了解子串的结构，首先要弄清楚几个概念:前缀、后缀和部分匹配值。

前缀指除最后一个字符以外，字符串的所有头部子串；

后缀指除第一个字符外，字符串的所有尾部子串；

部分匹配值则为字符串的前缀和后缀的最长相等前后缀长度。

下面以’ ababa’为例进行说明:

• ‘a’ 的前缀和后缀都为空集，最长相等前后缀长度为0。
• ‘ab’ 的前缀为{a)，后缀为{b}，{a}n{b} =，最长相等前后缀长度为0。
• 'aba’的前缀为{a,ab}，后缀为{a,ba}，{a,ab)n{a, ba}={a)，最长相等前后缀长度为l。
• 'abab’的前缀{a,ab,aba}n后缀{b,ab,bab}={ab}，最长相等前后缀长度为2。
• 'ababa '的前缀{a,ab,aba,abab}n后缀{a, ba,aba,baba}={a,aba}，公共元素有两个，最长相等前后缀长度为3。

故字符串’ ababa’的部分匹配值为 00123。

（二）、由部分匹配值得到next数组

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	0	0	1	0

对算法的改进方法:
已知:右移位数 = 已匹配的字符数 - 对应的部分匹配值（PM）。

写成:Move=(j-1)-PM[j-1]。

使用部分匹配值时，每当匹配失败，就去找它前一个元素的部分匹配值，这样使用起来有些不方便，所以将PM表右移一位，这样哪个元素匹配失败，直接看它自己的部分匹配值即可。
将上例中字符串’abcac’的PM表右移一位，就得到了next数组:

编号	1	2	3	4	5
S	a	b	c	a	c
PM	-1	0	0	0	1

我们注意到:
1）第一个元素右移以后空缺的用-1来填充，因为若是第一个元素匹配失败，则需要将子串向右移动一位，而不需要计算子串移动的位数。
2）最后一个元素在右移的过程中溢出，因为原来的子串中，最后一-个元素的部分匹配值是其下一个元素使用的，但显然已没有下一个元素，故可以舍去。

这样，上式就改写为

Move=(j-1)-next[j-1]

相当于将子串的比较指针j回退到

j=j-Move=j-((j-1)-next [j] )=next.[j]+1

有时为了使公式更加简洁、计算简单，将next数组整体+1。.因此，上述子串的next数组也可以写成

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	1	1	1	2

最终得到子串指针变化公式 j = next[j]。在实际匹配过程中，子串在内存里是不会移动的,而是指针在变化，书中画图举例只是为了让问题描述得更加形象。

next[j] 的含义是：在子串的第 i 个字符与主串发生失配时，则跳到子串的next[j] 位置重新与主串当前位置进行比较。

通过上述分析可以得出 next 函数的公式：

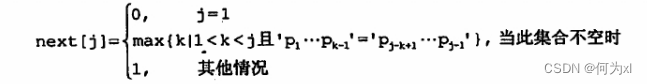
2. 算法编程实现

#define MAXLEN 255      //预定义最大串长为255
typedef struct {
    char ch[MAXLEN];    //每个分盘存储一个字符
    int length;         //串的实际长度
) SString;

next 数组的算法实现：

void get_next(SString T, int *next){
　　int i = 1;
　　int j = 0;
    next[1] = 0;
　　while (i < T.length){
　　　　if (j==0 || T.ch[i] == T.ch[j]) {
　　　　　　++i;
　　　　　　++j;
　　　　　　next[i] = j;
　　　　}　　　　
        else　　　　
　　　　　　j = next[j];
　　}
}

基于next的KMP算法的实现：

int Index_KMP(SString s,SString T,int next[] ){
    int i=1, j=1;
    while( i <= s.length && j <= T.length){
        if(j==0 || s.ch[i] == T.ch[j]){
            ++i;
            ++j;//继续比较后继字符           
        }
        else
            j=next[j];  //模式串向右移动
    }
    if(j>T.length)
        return i-T.length;  //匹配成功
    else
        return 0;
}

性能分析

尽管普通模式匹配的时间复杂度是O(mn)，KMP 算法的时间复杂度是Om+n)，但仕双俏况下，普通模式匹配的实际执行时间近似为O(m +n)，因此至今仍被采用。KMP算法仅在主串与子串有很多“部分匹配”时才显得比普通算法快得多，其主要优点是主串不回溯。

最坏时间复杂度：Om+n)
其中，求 next 数组时间复杂度为 O(m),模式匹配过程最坏时间复杂度 O(n)

3. 进一步优化 —— nextval 数组

4. KMP 算法完整代码：

注：由于时间关系，此代码摘自
https://www.cnblogs.com/ciyeer/p/9035072.html

#include <stdio.h>
#include <string.h>
void Next(char *T, int *next){
　　int i = 1;
　　next[1] = 0;
　　int j = 0;
　　while (i<strlen(T)) 　　{
　　　　if (j==0 || T[i-1]==T[j-1]) 　　　　{
　　　　　　i++;
　　　　　　j++;
　　　　　　next[i] = j;
　　　　}　　　　else　　　　{
　　　　　　j = next[j];
　　　　}
　　}
}
int KMP(char *S, char *T){
　　int next[10];
　　Next(T, next);　　//根据模式串T,初始化next数组
　　int i = 1;
　　int j = 1;
　　while (i<=strlen(S)&&j<=strlen(T)) 　　{
　　　　//j==0:代表模式串的第一个字符就和当前测试的字符不相等；S[i-1]==T[j-1],如果对应位置字符相等，两种情况下，指向当前测试的两个指针下标i和j都向后移
　　　　if (j==0 || S[i-1]==T[j-1]) 　　　　{
　　　　　　i++;
　　　　　　j++;
　　　　}
　　　　else　　　　{
　　　　　　j = next[j];//如果测试的两个字符不相等，i不动，j变为当前测试字符串的next值
　　　　}
　　}
　　if (j>strlen(T)) 　　{　　　　//如果条件为真，说明匹配成功
　　　　return i-(int)strlen(T);
　　}
　　return -1;
}
int main() {
　　int i = KMP("ababcabcacbab", "abcac");
　　printf("%d", i);
　　return 0;
}
运行结果：
6

注意：在此程序中，next 数组使用的下标初始值为 1 ，next[0] 没有用到（也可以存放 next 数组的长度）。而串的存储是从数组的下标 0 开始的，所以程序中为 T[i-1] 和 T[j-1]。