HDU 5073 Galaxy 【贪心】

最新推荐文章于 2021-08-04 15:15:41 发布

心悦灵溪

最新推荐文章于 2021-08-04 15:15:41 发布

阅读量240

点赞数

CC 4.0 BY-SA版权

分类专栏：贪心

本文链接：https://blog.youkuaiyun.com/weixin_43847416/article/details/95887016

贪心专栏收录该内容

27 篇文章

订阅专栏

传送门：HDU 5073

Galaxy Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)

Problem Description
Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.
在这里插入图片描述
To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.
Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.
The moment of inertia I of a set of n stars can be calculated with the formula
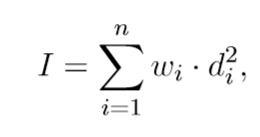
在这里插入图片描述
where wi is the weight of star i, di is the distance form star i to the mass of center.
As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.
Now, you are supposed to calculate the minimum moment of inertia after transportation.

Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.

Output
For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.

Sample Input
2
3 2
-1 0 1
4 2
-2 -1 1 2

Sample Output
0
0.5

题意：

一共有n个星球，每个星球质量相同且为1，这些星球围绕着其中心旋转，你可以去掉最多K个星球，使得其最后的：
惯性矩：I= $\displaystyle\sum_{i=1}^{n}w_i*d_i^2$ 的值最小，其中d_i表示第i个点到中心的距离,w_i表示每个星球的质量，按题意质量均为1。

注：随着点的去掉，中心一定是不同的。如样例-2 -1 1 2，如果去除-2 -1，那么中心为1.5；如果去除-2 2，那么中心为0。

题解：

1.我们假设去掉t个点后，中心点的坐标为x，那么惯性矩I= $\displaystyle\sum_{i=1}^{n-t}{(d_i-x)^2}$ ;那么中心点的坐标怎么求？不难看出就是剩余点的平均值。那么惯性矩I不就是剩余点的方差吗？

2.我们接下来考虑方差的特性。方差是表示事物离散程度的量，他满足：点越少，点越密集，值越小。题目说我们可以删除至多k个点，按照方差的性质，我们一定是删除k个点的，那么问题是我们怎么使剩余是n-k个点更密集？

首先我们可以确定一点：连续的点一定比不连续的点密集，所有我们剩余的点一定是连续的。

我们先将所有星球的坐标由小到大排序，假设为[1,2,4,5,7,9,10],k=4;
那么去除k个点后，我们可以选择的区间为：
[1 2 4 5],[2 4 5 7],[4 5 7 9],[5 7 9 10]

如果我们暴力搜一遍，那么时间复杂度为O(n²),肯定会超时，所有我们需要优化一下。
在这里插入图片描述

我们观察式子I= $\displaystyle\sum_{i=1}^{n-k}{(d_i-x)^2}$ ，可以拆开，变成：
I= $\displaystyle\sum_{i=1}^{n-k}{d_i^2}$ - $\displaystyle\sum_{i=1}^{n-k}{2*x*d_i}$ + $\displaystyle\sum_{i=1}^{n-k}{x^2}$

= $\displaystyle\sum_{i=1}^{n-k}{d_i^2}$ - $2 * x$ $\displaystyle\sum_{i=1}^{n-k}{d_i}$ + $n-k)*x^2$

对于每个区间，中心x的坐标为定值，n-k为定值，只有d_i和d_i*d_i的合不确定，我们只要用两个数组存d_i和d_i*d_i的前缀和，便可将时间优化为O(n).

我一开始觉得对于每个连续的区间，只要把他们的起点变成一样的，因为长度相同，只有看谁的总和更小，谁的方差就是最小的了，但是我没考虑到如果总和相等怎么求，结果wa了，TAT

AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#define ll long long
#define inf 0x3f3f3f3f//1061109567
using namespace std;
const int N=100000;
int t,n,k;
ll r[N],sum1[N],sum2[N];
int main()
{
  scanf("%d",&t);
  while(t--)
  {
    memset(sum1,0,sizeof(sum1));
    memset(sum2,0,sizeof(sum2));
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
    {
      scanf("%I64d",&r[i]);
    }
    sort(r+1,r+n+1);
    for(int i=1;i<=n;i++)
    {
      sum1[i]=sum1[i-1]+r[i];
      sum2[i]=sum2[i-1]+r[i]*r[i];
    }
    double minn=1e14,ans=0;//最小值初始化得足够大
    for(int i=n-k;i<=n;i++)
    {
      ll num=sum1[i]-sum1[i-n+k];
      double temp=num*1.0/(n-k)*1.0;
      ans=sum2[i]-sum2[i-n+k]-2*temp*num+(n-k)*temp*temp;
      minn=min(minn,ans);
    }
    if(n==k) minn=0;
    printf("%.10lf\n",minn);
  }
  return 0;
}