HDU 5536 Chip Factory

题目链接

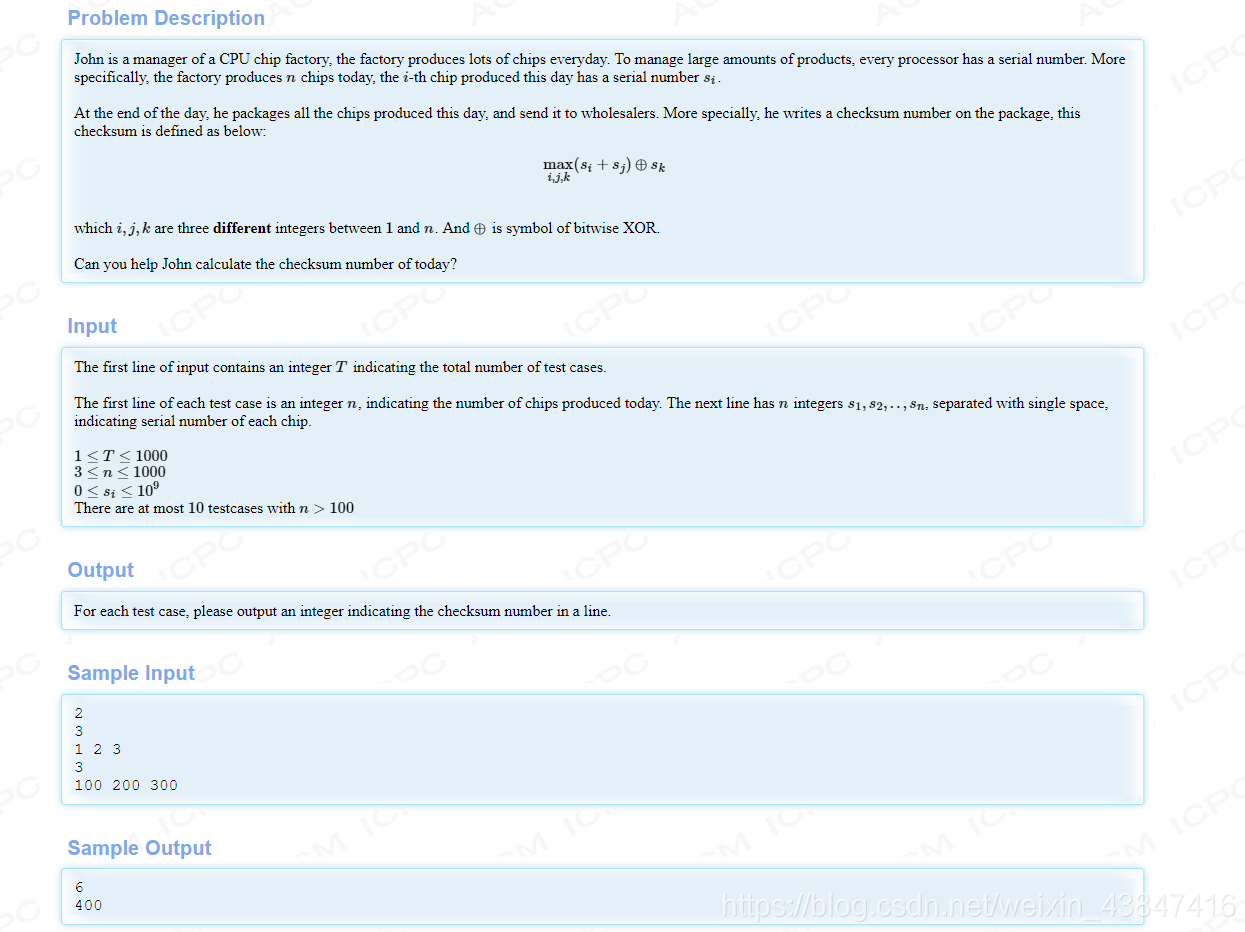
题目大意：
在一个数组中找出 (s[i]+s[j])^s[k] 最大的值，其中 i、j、k 各不相同。

思路：
求异或结果最大很容易想到01字典树，01字典树可以解决查找与 x 异或结果最大的数和结果值。本题由于数据很小(3<=n<=1000)，所以可以两层循环求出两个不同数的和，然后在剩余的数中用 01字典树求与它们的和异或最大的结果值。

问题在于我们如果确定下标不同。我们可以设置一个数组num，用来记录每个结点被访问的次数，我们只要每次改变结点的访问次数即可控制下标不同，具体操作看代码。

注意：
题目要求的数据超过了int的范围，所以要用long long型。

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int MAXN=1100;
int n,m,t;
ll a[MAXN];
int trie[32*MAXN][2];
ll val[32*MAXN];//结点值
int num[32*MAXN];//每个结点被访问的次数
int tot;
void insert(ll d)
{
    int root=0;
    for(int i=32;i>=0;i--)
    {
        int id=(d>>i)&1;//获得这一个bit位的值
        if(!trie[root][id]) trie[root][id]=++tot;
        root=trie[root][id];
        num[root]++;
    }
    val[root]=d;
}
void update(ll x,ll add)//更新插入或删除x后每个结点被访问的次数
{
  int root=0;
  for(int i=32;i>=0;i--)
  {
    int id=(x>>i)&1;
    root=trie[root][id];
    num[root]+=add;
  }
}
ll query(ll d)//查询所有数中和d异或结果最大的数
{
    int root=0;
    for(int i=32;i>=0;i--)
    {
        int id=(d>>i)&1;
        //利用贪心策略，优先寻找和当前位不同的数
        if(trie[root][id^1]&&num[trie[root][id^1]]) root=trie[root][id^1];
        else root=trie[root][id];
    }
    return d^val[root];
}
int main()
{
  scanf("%d",&t);
  while(t--)
  {
    ll ans=0;
    tot=0;//注意初始化
    memset(num,0,sizeof(num));
    memset(trie,0,sizeof(trie));
    memset(val,0,sizeof(val));
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
      scanf("%lld",&a[i]);
      insert(a[i]);
    }
    for(int i=0;i<n;i++)
    {
      for(int j=0;j<n;j++)
      {
        if(i==j) continue;
        update(a[i],-1);
        update(a[j],-1);
        ans=max(ans,query(a[i]+a[j]));
        update(a[i],1);
        update(a[j],1);
      }
    }
    printf("%lld\n",ans);
  }
  return 0;
}