回溯法之N皇后问题(四皇后)

回溯法（英语：backtracking）是暴力搜寻法中的一种。
回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。

n皇后问题：
就是nxn的国际象棋棋盘上，逐行放置皇后，要求每一行，每一列，每一条斜线都只能放置一个皇后。

回溯过程分析：
1.从空棋盘起，逐行放置棋子
2.每在一个布局中放下一个棋子，即推演到一个新的布局
3.如果当前行上没有可合法放置棋子的位置，则回溯当上一行，重新布放上一行的棋子。

以四皇后为例，给出回溯的求解过程图：

数据结构分析：
1.二位数组A[N][N]存储皇后位置，若第i行第j列有皇后，则A[N][N]为非0值，否则值为0.
2.一位数组M[k]、L[k]、R[k]分别表示竖列、左斜线、右斜线是否放有皇后，有则值为1，否则值为0.

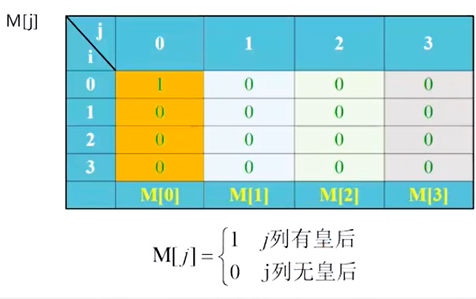
j列上放置皇后时，M[j]=1，否则为0；

左斜线上，i+j的值一致，一共7条斜线(2N-1),对应L数组中的7个位置，比如说A[2][3]=1,也就是说第2行3列放置皇后，则L[i+j]=L[5]=1，表示第5+1=6条左斜线有一个皇后。

右斜线上，i-j的值一致，由于会出现负值，所以i-j+N，处理成正值，一共7条斜线(2N-1),对应R数组中的7个位置，比如说A[2][3]=1,也就是说第2行3列放置皇后，则L[i-j+N]=L[-1+4]=L[3]=1，表示第3条右斜线有一个皇后。

#include<stdio.h>
#include<stdlib.h>
#define N 100
int a[N][N]={0};//用来保存象棋布局，a[i][j]为0表示没有放置皇后，为非0值表示放置皇后
int M[N]={0};//M[j]=0表示第j列没有皇后，=1表示第j列已经放置了皇后
int L[N]={0};//L[j]=0表示第j条左斜线上没有皇后，=1表示第j条左斜线已经放置了皇后
int R[N]={0};//R[j]=0表示第j条右斜线上没有皇后，=1表示第j条右斜线已经放置了皇后
int n;//n皇后问题，n x n棋盘
int num;
int count;

void print()
{
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			printf("%d ",a[i][j]);
		}
		printf("\n");
	}
}

int solve(int i)
{
	for(int j=0;j<n;j++)
	{
		if(!M[j] && !L[i+j] && !R[i-j+n])//检查某一列，某一斜线上只有一个皇后
		{
			a[i][j]=i+1;
            M[j]=L[i+j]=R[i-j+n]=1;
            if(i==n-1)//逐行放置皇后，当放到最后一行的时候输出
            {
            	printf("\n");
            	print();
            	count++;
            }
            else
            {
            	solve(i+1);
            }
            a[i][j]=0;//去除皇后，回退
            M[j]=L[i+j]=R[i-j+n]=0;
		}
	}
	return count;
}
int main()
{
	scanf("%d",&n);
	num=solve(0);
	printf("%d\n",num);
}