单高斯模型(GSM)
高斯模型是一种常用的变量分布模型, 而且有很好的数学性质,具有各阶导数,变量频数分布由 μ、σ 完全决定等等,在许多领域得到广泛应用。它的概率密度分布函数如下:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲f \left ( x \ri…
μ 和σ2{\sigma ^2}σ2分别是高斯分布的均值和方差。譬如将男生身高视为变量X, 假设男生的身高服从高斯分布,则X∼N(μ,σ2)X \sim N(\mu ,{\sigma ^2})X∼N(μ,σ2),女生亦如此。只是男女生身高分布可能具有不同的均值和方差。图1是从谷歌图库中搜索到的男女生身高分布图。
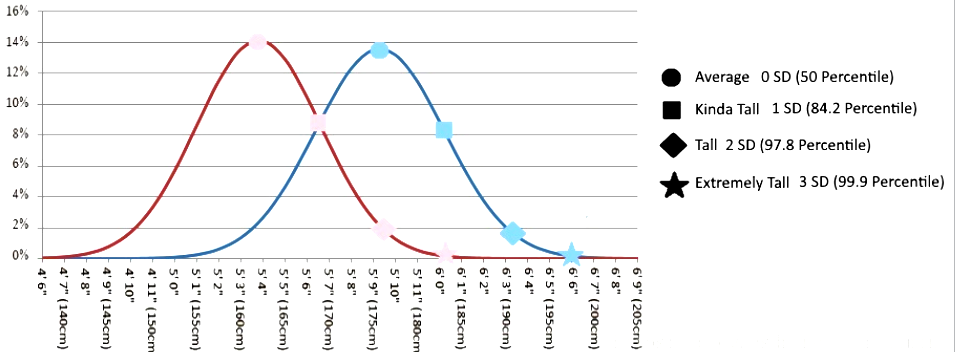
其中:
d:变量维度。对于二维高斯分布,有d=2;
u=(u1u2...un)u = \left( \begin{array}{l}{u_1}\\{u_2}\\...\\{u_n}\end{array} \right)u=⎝⎜⎜⎛u1u2...un⎠⎟⎟⎞:各维变量的均值;
Σ :协方差矩阵,描述各维变量之间的相关度。对于二维高斯分布,有:
Σ=[δ11δ12δ21δ22] \Sigma= \left[\begin{matrix}\delta _{11} & \delta _{12} \\ \delta _{21}&\delta _{22} \end{matrix}\right] Σ=[δ11δ21δ12δ22]
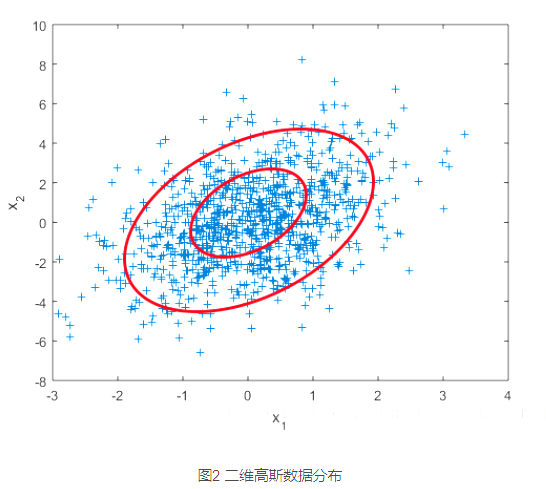
图2是二维高斯分布产生的数据示例,参数设定为:u=(00),Σ=[10.80.85]u = \left( \begin{array}{l}0\\0\end{array} \right),\Sigma= \left[\begin{matrix}1 & 0.8\\0.8&5 \end{matrix}\right]u=(00),Σ=[10.80.85]。 服从二维高斯分布的数据主要集中在一个椭圆内部,服从三维的数据集中在一个椭球内部。
参数对二维高斯分布的影响
u=(00),Σ=[3003]u = \left( \begin{array}{l}0\\0\end{array} \right),\Sigma= \left[\begin{matrix}3 & 0\\0&3 \end{matrix}\right]u=(00),Σ=[3003]
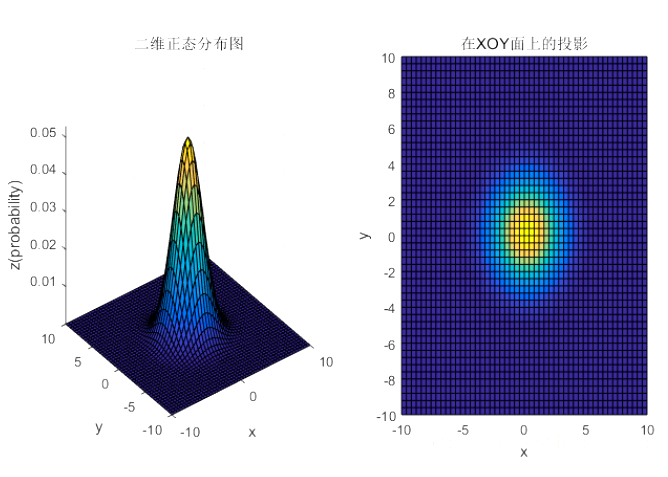
u=(44),Σ=[3003]u = \left( \begin{array}{l}4\\4\end{array} \right),\Sigma= \left[\begin{matrix}3 & 0\\0&3 \end{matrix}\right]u=(44),Σ=[3003]
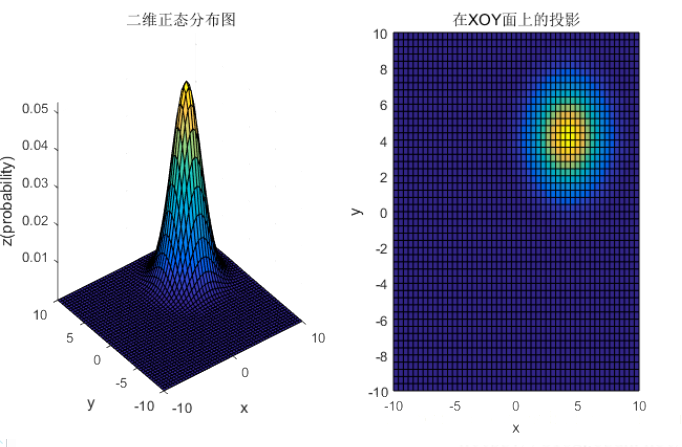
u=(00),Σ=[30010]u = \left( \begin{array}{l}0\\0\end{array} \right),\Sigma= \left[\begin{matrix}3 & 0\\0&10 \end{matrix}\right]u=(00),Σ=[30010]
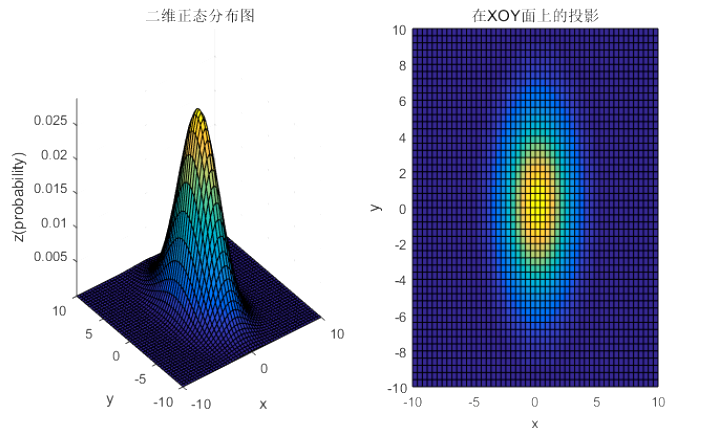
u=(00),Σ=[10.80.81]u = \left( \begin{array}{l}0\\0\end{array} \right),\Sigma= \left[\begin{matrix}1 & 0.8\\0.8&1 \end{matrix}\right]u=(00),Σ=[10.80.81]
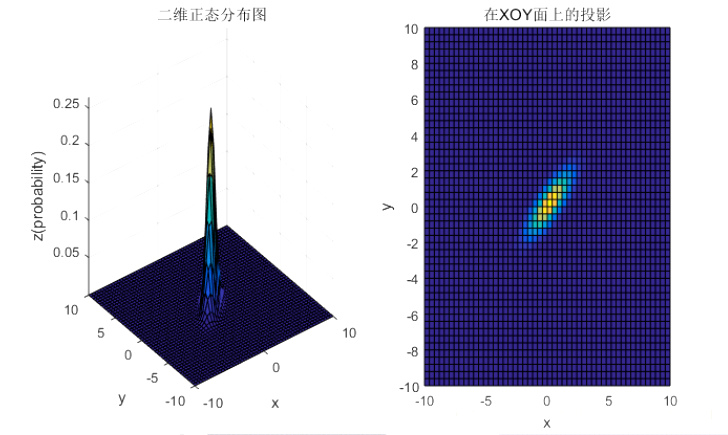
u=(00),Σ=[1−0.8−0.81]u = \left( \begin{array}{l}0\\0\end{array} \right),\Sigma= \left[\begin{matrix}1 & -0.8\\-0.8&1 \end{matrix}\right]u=(00),Σ=[1−0.8−0.81]
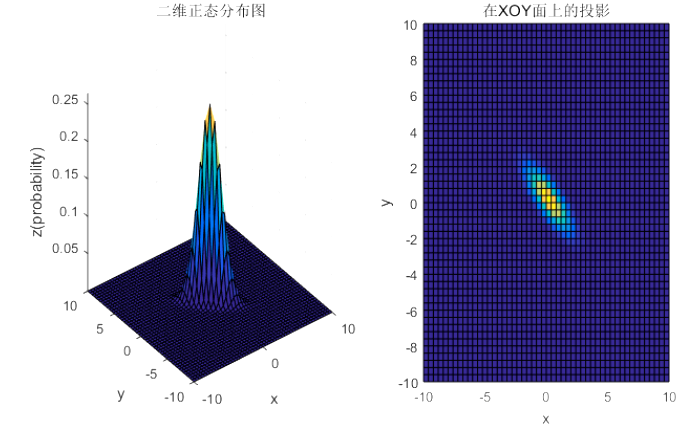
① 均值表征的是各维变量的中心,其对二维高斯曲面的影响较好理解,它使得整个二维高斯曲面在XoYXoYXoY平面上移动;
② 对于协方差矩阵,对角线上的两个元素,即δ11δ_{11}δ11和δ22δ_{22}δ22表征的是x维和y维变量的方差,决定了整个高斯曲面在某一维度上的“跨度”,方差越大,“跨度”越大;
③ 协方差矩阵的斜对角线上面的两个元素,即δ12δ_{12}δ12和δ21(δ12=δ21)δ_{21}(δ_{12}=δ_{21})δ21(δ12=δ21)表征的是各维变量之间的相关性:δ12>0δ_{12}>0δ12>0说明x与y呈正相关(x越大,y越大),其值越大,正相关程度越大;δ12<0δ_{12}<0δ12<0呈负相关;否则不相关。
混合高斯模型(GMM)
模型引入
先看一组数据
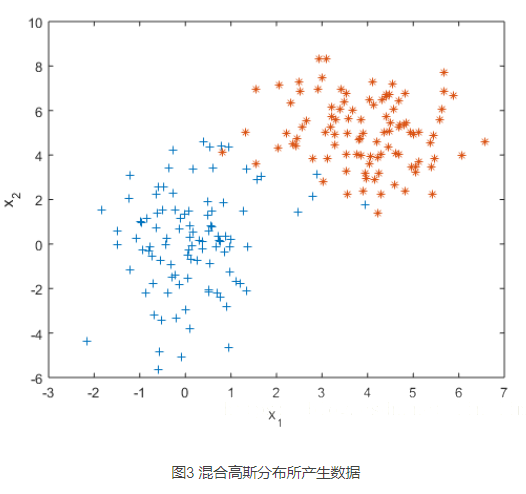
如果我们假设这组数据是由某个高斯分布产生的,利用极大似然估计对这个高斯分布做参数估计,得到一个最佳的高斯分布模型如下。
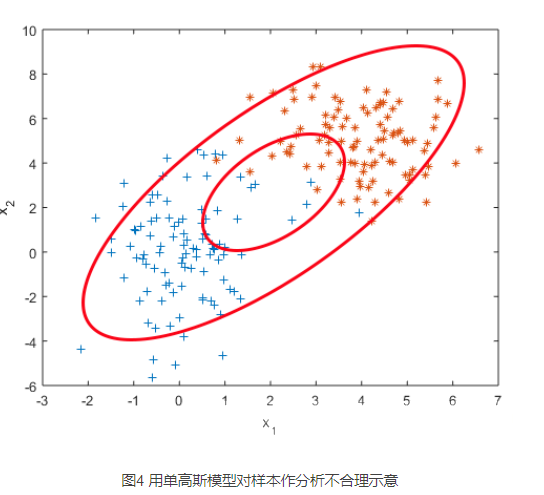
一般来讲越靠近椭圆的中心样本出现的概率越大,这是由概率密度函数决定的,但是这个高斯分布的椭圆中心的样本量却极少。显然样本服从单高斯分布的假设并不合理。单高斯模型无法产生这样的样本。实际上,用两个不同的高斯分布模型会有更合理的效果。
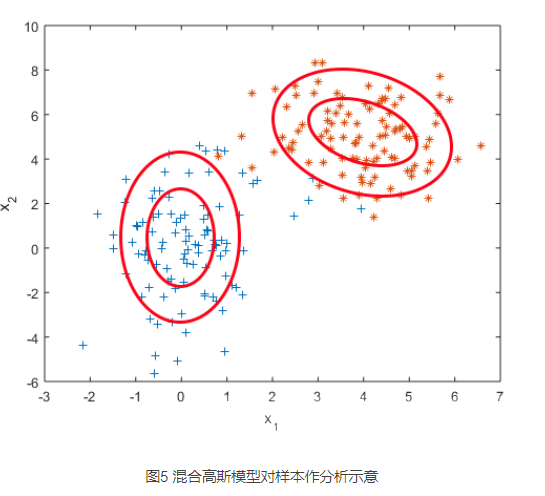
它通过求解两个高斯模型,并通过一定的权重将两个高斯模型融合成一个模型,即最终的混合高斯模型。这个混合高斯模型可以产生这样的样本。更一般化的描述为:假设混合高斯模型由K个高斯模型组成(即数据包含K个类),则GMM的概率密度函数如下:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲P(x)=\sum_{k=1}…
其中,








 本文详细介绍了EM算法和高斯混合模型(GMM)。首先讲解了单高斯模型及其参数对二维高斯分布的影响,接着讨论了混合高斯模型的引入和直观理解,指出其能更好地拟合复杂数据。然后,文章深入探讨了极大似然估计(MLE)以及在解决混合模型参数估计问题时遇到的困难,最终引入EM算法,包括E-step和M-step,并通过示例展示了EM算法的优化过程。整个文章旨在帮助读者理解EM算法在GMM中的应用。
本文详细介绍了EM算法和高斯混合模型(GMM)。首先讲解了单高斯模型及其参数对二维高斯分布的影响,接着讨论了混合高斯模型的引入和直观理解,指出其能更好地拟合复杂数据。然后,文章深入探讨了极大似然估计(MLE)以及在解决混合模型参数估计问题时遇到的困难,最终引入EM算法,包括E-step和M-step,并通过示例展示了EM算法的优化过程。整个文章旨在帮助读者理解EM算法在GMM中的应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 367
367

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








