查准率、查全率、P-R图与F1值

1.查准率、查全率与P-R图

以西瓜问题为例，假定农夫拉来一车西瓜，我们用训练好的模型对西瓜进行判别，错误率可以衡量有多少比例的瓜被判别错误。但是我们关心的是“挑出的西瓜中有多少比例是好瓜”，或者“所有的好瓜中有多少被挑出来”，这时候就涉及到"查准率"与"查全率"。（选自西瓜书）

对于二分类问题，根据样本的真实类别与学习器预测类别的组合可以分为真正例（true positive，TP）、假正例（false positive，FP）、真反例（true negative，TN）和假反例（false negative，FN），其中的真假表示分类是否准确，正反表示学习器预测类别。例如假正例表示预测错误并且预测类别为正，即实际类别为负。显然有TP+FP+TN+FN=样本总数。分类结果混淆矩阵如下：

                     

 由此定义查准率与查全率：

                                          

            查准率P=TP/(TP+FP)        （所有预测为正的样本中，有多少实际为正）

            查全率R=TP/(TP+FN)        （所有实际为正的样本中，有多少被挑出）

查准率与查全率是一对矛盾的度量；一般来说查全率高时，查准率会偏低，反之亦然。例如：希望将好瓜尽可能地选出来，可通过选瓜的数量来实现；如果将所有的西瓜都选上，那么所有的好瓜也必然选上，但这时候查准率就会降低。

 很多情形下，我们可以根据学习器的预测结果（即学习器预测为正例的概率）对样本进行排序，排在前面的是学习器认为“最可能”是正例的样本，最后的则是学习器认为最不可能是正例的样本。按照此顺序逐个把样本作为正例进行预测，则每次都可计算出当前的查全率和查准率。以查准率为纵轴、查全率为横轴作图，得到查准率-查全率曲线，简称“P-R曲线”,给出一个示意图如下：

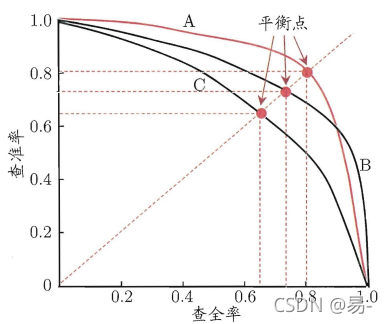
P-R曲线

以一个例子说明P-R图的绘制过程：

假设用（x，y）的形式表示样本，其中x表示学习器输出的概率大小，y表示样本实际类别。现有四个样本分别为a(0.85，+)、b(0.55，-)、c(0.45，+)、d(0.15，-)

1.以0.80为阈值，若a>0.8则预测为正例，否则为负例。结果是a预测为+，bcd预测为-，此时查准率为1，查全率为1/2；

2.以0.50为阈值，若a>0.5则预测为正例，否则为负例。结果是ab预测为+，cd预测为-，此时查准率为1/2，查全率为1/2；

3.以0.40为阈值，若a>0.4则预测为正例，否则为负例。结果是abc预测为+，d预测为-，此时查准率为2/3，查全率为1；

4.以0.10为阈值，若a>0.1则预测为正例，否则为负例。结果是abcd预测为+，此时查准率为1/2，查全率为1；

将上述的四个点描入P-R曲线并相连就能得到P-R曲线。

2.F1值

P-R图直观地显示出学习器在样本总体上的查全率、查准率。在进行学习器性能比较时，若一个学习器的P-R曲线完全包住另一个学习器的曲线，则断言前者的性能优于后者。在上图中，学习器A的性能优于学习器C。但是当两个学习器的P-R曲线发生交叉时，例如图中的A与B，则难以判断两个学习器的好坏。若要将AB两个学习器比较高低，一种合理的判据是比较P-R曲线下的面积大小，它在一定程度上表征了学习器在查准率和查全率上取得相对“双高”的比例。但是这个值不太容易估计，因此人们设计了一些综合考虑查全率与查准率的性能度量。

“平衡点（BEP）”就是一种度量方式，它是“查准率=查全率”时的取值。在上图中，基于BEP的比较，可认为学习器A优于B。但是BEP过于简单，更常用的是F1度量：

                                 

 F1是基于查准率与查全率的调和平均数：

在一些实际应用中，对查准率与查全率的重视程度不同。例如在商品推荐系统中，为了尽可能不打扰用户，更希望推荐内容就是用户感兴趣的，此时查准率更重要；而在逃犯追捕中，更希望尽可能少漏掉逃犯，此时查全率更重要。根据对查准率/查全率的不同偏好，它的一般形式定义为：

                                 

Fß是基于查准率和查全率的加权调和平均数：

其中 ß>1时查全率有更大影响；ß<1时查准率有更大影响。

参考资料：《机器学习》周志华著，清华大学出版社