完整的实验代码在我的github上👉QYHcrossover/ML-numpy: 机器学习算法numpy实现 (github.com) 欢迎star⭐
决策树算法是一种经典的机器学习算法,它在许多领域都有广泛的应用。决策树模型通过树形结构来表示不同的决策路径,每个节点代表一个特征变量,每个分支代表一个可能的取值。决策树模型是一种可解释性强的模型,它不仅可以用于分类问题,还可以用于回归问题。本文将介绍决策树算法的原理,并通过实例演示如何使用ID3算法构建决策树模型。
决策树算法原理
决策树是一种常用的分类和回归算法,其原理是通过不断地选择最佳分裂特征和阈值来构建一棵树形结构,从而对数据进行分类或预测。决策树的构建过程类似于一个问题的“筛选”过程,通过不断地提出问题和根据问题的答案将样本分割成不同的子集,最终将样本分到相应的类别或预测出其对应的数值。
决策树的构建是一个自上而下的递归过程,具体来说,它包含以下几个步骤:
- 特征选择:选择最优的特征作为当前节点的划分属性,使得划分后的各个子节点尽可能地“纯净”。
- 节点划分:按照选定的特征将当前节点的样本集划分为多个子节点,每个子节点对应于选定特征的不同取值。
- 递归构建:对每个子节点递归地执行上述步骤,直到满足终止条件,如节点中的样本数小于预定阈值,节点中的样本属于同一类别等。
决策树算法的原理其实就是不断地对特征进行选择和节点的划分,最终生成一个决策树模型,用于对新的样本进行分类或回归。
ID3算法是决策树算法中的一种,它基于信息增益来选择特征。信息增益的概念是在信息论中提出的,它表示在已知一个事件发生的前提下,该事件所提供的信息量。ID3算法通过计算每个特征的信息增益来选择分裂特征。这种方法的缺点是它倾向于选择取值数目较多的特征作为分裂特征,因此它的决策树往往比较深,容易出现过拟合的问题。ID3算法的信息增益计算公式为:

C4.5算法是ID3算法的改进版,它引入了增益率的概念,即用特征的信息增益比来选择分裂特征。增益率解决了ID3算法中倾向选择取值数目较多的特征的问题,因此它生成的决策树通常比ID3算法的决策树要浅,泛化性能也更好。此外,C4.5算法还可以处理缺失值和连续特征,它使用一种叫做“二分法”的方法将连续特征离散化,然后再按照离散化后的取值进行划分。C4.5算法的增益率计算公式为:
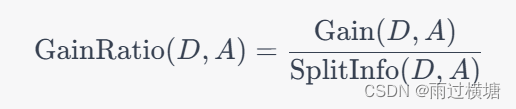
其中, SplitInfo ( D , A ) \operatorname{SplitInfo}(D, A) SplitInfo(D,A)为特征 A A A的分裂信息,表示对数据集 D D D进行特征 A A A划分的难易程度。 SplitInfo ( D , A ) \operatorname{SplitInfo}(D, A) SplitInfo(D,A)越大,表示特征 A A A的分裂能力越弱。
ID3代码实践
from sklearn.model_selection import train_test_split
import numpy as np
from collections import Counter
class ID3DecisionTree:
@staticmethod
def entropy(y):
precs = np.array(list(Counter(y).values()))/len(y)
ent = np.sum(-1 * precs * np.log(precs))
return ent
def decide_feature(self,X,y,feature_order):
n_features = X




 本文介绍了决策树算法的原理,通过不断选择最佳分裂特征进行数据划分,构建可解释性强的分类模型。详细讲解了ID3算法,包括信息增益的概念,以及如何用Python实现ID3算法。最后,简要提到了CART算法作为ID3的改进版,使用基尼系数选择特征。
本文介绍了决策树算法的原理,通过不断选择最佳分裂特征进行数据划分,构建可解释性强的分类模型。详细讲解了ID3算法,包括信息增益的概念,以及如何用Python实现ID3算法。最后,简要提到了CART算法作为ID3的改进版,使用基尼系数选择特征。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1673
1673










