数据结构：一文看懂二叉搜索树 （JavaScript）

二叉搜索树介绍

1. 二叉搜索树是一种节点值之间具有一定数量级次序的二叉树，对于树中每个节点：
2. 若其左子树存在，则其左子树中每个节点的值都不大于该节点值；
3. 若其右子树存在，则其右子树中每个节点的值都不小于该节点值。

满足条件

1. 若左子树不为空，则左子树上左右节点的值都小于根节点的值；
2. 若它的右子树不为空，则它的右子树上所有的节点的值都大于根节点的值；
3. 它的左右子树也要分别是二叉搜索树；

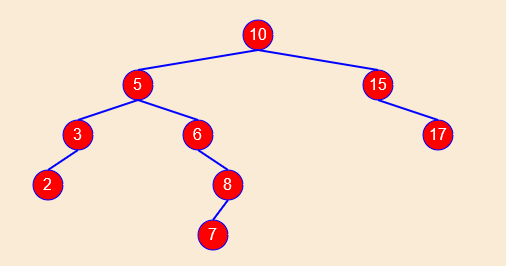
查询节点过程是，比较元素值是否相等，相等则返回，不相等则判断大小情况，迭代查询左、右子树，直到找到相等的元素，或子节点为空，返回节点不存在。

两种特殊的二叉树

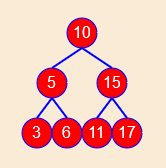
完全二叉树，所有节点尽量填满树的每一层，上一层填满后还有剩余节点的话，则由左向右尽量填满下一层。

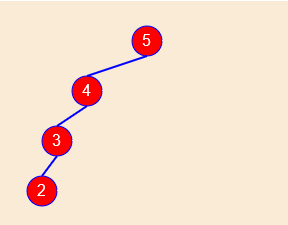
每一层只有一个节点的二叉树。

Node节点实例

let Node = function (key) {
   
   
    this.key = key;
    this.left = null;
    this.right = null;
}
this.roots = null;

实例一个节点

let node = new Node()
console.log(node)
//{ key: undefined, left: null, right: null }

1.二叉树插入

1.1Node节点实例

//Node节点实例
function Node(key) {
   
   
    this.key = key;
    this.left = null;
    this.right = null;
}

1.2二叉树对象

function BinarySearchTree() {
   
   
    this.roots = null;
    this.insert = insert
}

1.3 节点插入（三种情况）

由于二叉搜索树的特殊性质确定了二叉搜索树中每个元素只可能出现一次，所以在插入的过程中如果发现这个元素已经存在于二叉搜索树中，就不进行插入。否则就查找合适的位置进行插入。

1.3.1 第一种情况：_root为空

直接插入，return true；

let insert = function (key) {
   
   
    let newNode = new Node(key)
    if (this.roots === null) {
   
   
        this.roots = newNode
    }
}

1.3.2 第二种情况：要插入的元素已经存在

如上面所说，如果在二叉搜索树中已经存在该元素，则不再进行插入，直接return false；不再让它插入；

function insertNode(node, newNode) {
   
   
    if(newNode.key === node.key){
   
   
        return false
    }
}

节点插入测试

可以看到节点2没有重复插入;

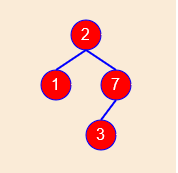
let BST = new BinarySearchTree();
BST.insert(2)
BST.insert(2)
BST.insert(7)
BST.insert(3)
BST.insert(1)
console.log(BST)

1.3.3 第三种情况：能够找到合适位置

function insertNode(node, newNode) {
   
   
    if(newNode.key === node.key){
   
   
        return false
    }
    if (newNode.key < node.key) {
   
   
        // 如果新节点值小于当前节点值，则插入左子节点
        if (node.left === null) {
   
   
            node.left = newNode
        } else {
   
   
            insertNode(node.left, newNode)
        }
    } else {
   
   
        // 如果新节点值小于当前节点值，则插入右子节点
        if (node.right === null) {
   
   
            node.right = newNode
        } else {
   
   
            insertNode(node.right, newNode)
        }
    }
}

1.3.4节点插入完整版

//Node节点实例
function Node(key) {
   
   
    this.key = key;
    this.left = null;
    this.right = null;
}
//二叉搜索树
function BinarySearchTree() {
   
   
    this.roots = null;
    this.insert = insert
}
let insert = function (key) {
   
   
    let newNode = new Node(key)
    if (this.roots === null) {
   
   
        this.roots = newNode
    } else {
   
   
        insertNode(this.roots, newNode)
    }
}
function insertNode(node, newNode) {
   
   
    if(newNode.key === node.key){
   
   
        return false
    }
    if (newNode.key < node.key) {
   
   
        // 如果新节点值小于当前节点值，则插入左子节点
        if (node.left === null) {
   
   
            node.left = newNode
        } else {
   
   
            insertNode(node.left, newNode)
        }
    } else {
   
   
        // 如果新节点值小于当前节点值，则插入右子节点
        if (node.right === null