Deep_Learning之反向传播

How the backpropagation algorithm works(反向传播算法是怎样运行的)

在上一章中，我们看到了神经网络如何使用梯度下降算法来学习它们的权值和偏差。然而，在我们的解释中有一个缺口:我们没有讨论如何计算成本函数的梯度。在这一章中，我将解释一种计算这种梯度的快速算法，一种称为反向传播的算法。
反向传播算法最初是在20世纪70年代引入的，但直到1986年David Rumelhart、Geoffrey Hinton和Ronald Williams的一篇著名论文才充分认识到它的重要性。那篇论文描述了几种神经网络，其中反向传播的工作速度远远快于早期的学习方法，使得使用神经网络来解决以前无法解决的问题成为可能。目前，反向传播算法是神经网络学习的主要工具。
这一章在数学上比本书的其余部分更复杂。如果您对数学不感兴趣，您可能会跳过这一章，并将反向传播视为一个您愿意忽略其细节的黑匣子。为什么要花时间研究这些细节呢?
原因当然是为了更好的理解。backpropagation的核心是cost function C的∂C/∂w对网络中任意权值w(或偏差b)的表达式。这个表达式告诉我们，当我们改变权重和偏差时，损失变化有多快。虽然这个表达有点复杂，但它也有一种美，每个元素都有一个自然、直观的解释。所以反向传播不仅仅是一种快速的学习算法。它实际上为我们提供了关于改变权重和偏差如何改变网络整体行为的详细见解。这很值得详细研究。
话虽如此，如果你想浏览这一章，或者直接跳到下一章，那也可以。我已经写了这本书的其余部分是可访问的，即使你把反向传播当作一个黑盒。当然，在本书后面的章节中，我提到了本章的结果。但在这些点上，你应该仍然能够理解主要的结论，即使你不遵循所有的推理。

Warm up: a fast matrix-based approach to computing the output from a neural network（热身:一种快速的基于矩阵的方法来计算神经网络的输出）

在讨论反向传播之前，让我们先使用一个快速的基于矩阵的算法来计算神经网络的输出。实际上，我们在上一章的最后已经简要地看到了这个算法，但是我很快地描述了它，所以值得详细地回顾一下。特别是，这是在熟悉的上下文中熟悉反向传播中使用的符号的好方法。
让我们从一个符号开始，它让我们以一种明确的方式引用网络中的权重。我们将使用wljk来表示从第(l−1)层的第k个神经元到第l层的第j个神经元之间连接的权值。例如，下图显示了网络中从第二层的第四个神经元到第三层的第二个神经元之间连接的权重:

这种表示法一开始很麻烦，需要花些功夫才能掌握。但是稍加努力，你就会发现这个符号变得简单而自然。这个符号的一个怪事是j和k指标的顺序。你可能认为用j表示输入神经元更有意义，用k表示输出神经元更有意义，而不是相反，就像实际做的那样。我将在下面解释这种怪事的原因。
我们使用类似的符号来表示网络的偏差和激活。明确地，我们用blj表示第j层神经元的偏置。我们用alj来激活第l层的第j个神经元。下图展示了这些符号的使用示例:

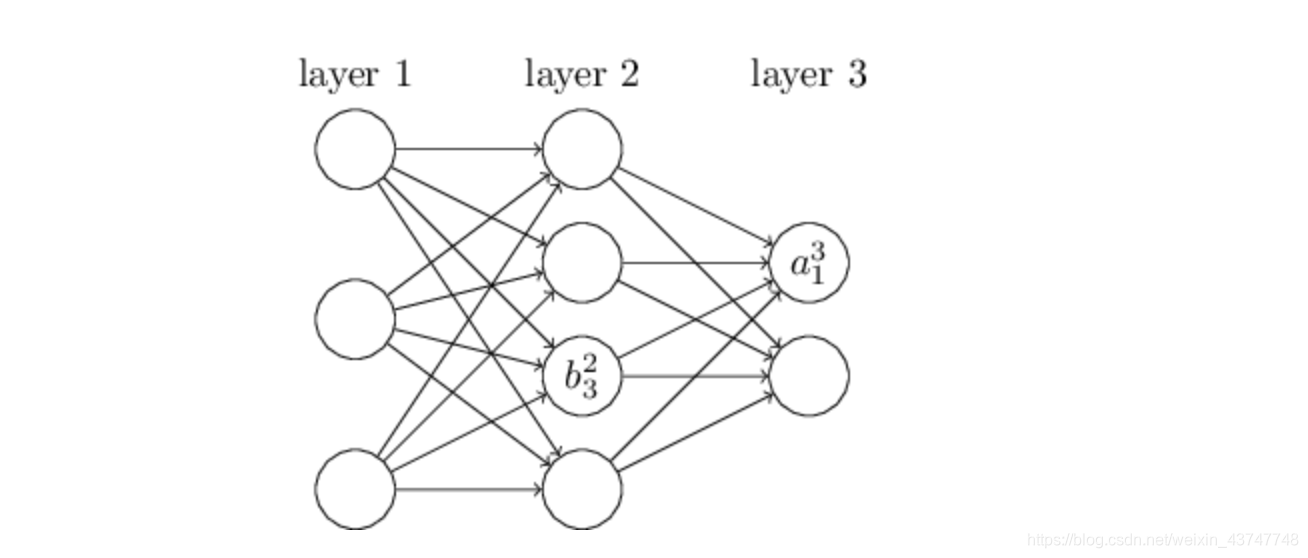
根据这些记号，第l层的第j个神经元的激活函数alj与l-1层的激活函数可以被写作为：

在每个vector上使用sigmoid函数：

也就是说，向量化的f只是对向量的每个元素进行了平方运算。
有了这些符号，方程(23)可以用漂亮而紧凑的矢量化形式重写

这个表达式给了我们一个更全局的思考如何一层与激活:

两个关于损失函数需要的2个假设（The two assumptions we need about the cost function）

The Hadamard product, s⊙t

The four fundamental equations behind backpropagation（反向传播背后的四个基本方程）

The backpropagation algorithm（反向传播算法）

The code for backpropagation

In what sense is backpropagation a fast algorithm?

Backpropagation: the big picture

正如我所解释的，反向传播呈现了两个谜团。首先，这个算法到底是干什么的?我们已经开发了从输出反向传播错误的图片。但是我们能再深入一点，建立更多的直觉当我们做这些矩阵和向量乘法的时候会发生什么?第二个谜团是，人们是如何发现反向传播的呢?遵循算法中的步骤是一回事，甚至遵循算法有效的证明也是一回事。但这并不意味着你很好地理解了这个问题，以至于你可以在一开始就发现这个算法。有没有一种合理的推理方法可以让你发现反向传播算法?在本节中，我将解决这两个问题。