Fibonacci

最新推荐文章于 2019-07-08 11:20:40 发布

原创最新推荐文章于 2019-07-08 11:20:40 发布 · 164 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#基础篇

算法笔记专栏收录该内容

36 篇文章

订阅专栏

本文探讨了斐波那契数列的计算方法，包括递归和迭代方式，并提出了一种使用数学公式计算大数值斐波那契数的方法，有效解决了递归计算在大数值下的效率问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

裴波那契数列

f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2] (i>=2)

#include<stdio.h>
int f(n)
{
	if(n==0)
		return 0;
	if(n==1)
		return 1;
	return f(n-1)+f(n-2);
}
int main()
{
	int n;
	while(scanf("%d",&n)!=EOF)
	{
		printf("%d\n",f(n));
	}
	return 0;
}

用这种方法运行到40左右就非常耗时

斐波那契数列的递推式

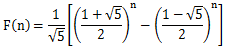
在这里插入图片描述
取得的不是准确数，裴波那契数越小精确度越差

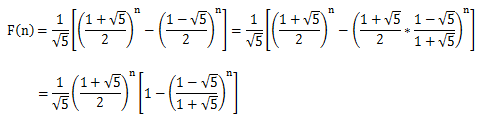
转化成这种格式计算更方便

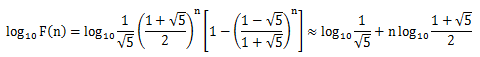
若想求裴波那契数列的前四项，可用这个公式，要先自己算出前20项（因为公式精确度不高），你可以先试一试求出的前20项的值与正确值是否相符。

#include<stdio.h>
#include<math.h>
int main()
{
	int i,n,f[21];
	double ans,x;    //要定义成double，担心精度不够
	f[0]=0;
	f[1]=1;
	for(i=2;i<=20;i++)
	f[i]=f[i-1]+f[i-2];
	while(scanf("%d",&n)!=EOF)
	{
		if(n<=20)
		{
			printf("%d\n",f[n]);
			continue;
		}
		x=sqrt(5);
		ans=log10(1.0/x)+n*log10((1+x)/2);
		ans=ans-(int)ans;    //求s的小数部分
		ans=pow(10.0,ans);   //求10的s次方
		while(ans<1000)
			ans*=10;
		printf("%d\n",(int)ans);    //只要整数部分
	}
	return 0;
}