2019牛客暑期多校训练营(六) J (DP) -Upgrading Technology_牛客多校 upgrading technology-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43720526/article/details/98729428

本文解析了一道算法题“升级技术”，探讨如何通过最优策略升级物品等级以获得最大收益。通过转换问题视角，将升级花费转为获得值，并采用枚举策略结合前缀和算法，求解最优解。文章详细介绍了算法思路、代码实现及常见错误点。

2019牛客暑期多校训练营（第六场）J-Upgrading Technology

题目描述

$\;\;\;\;\;$ 有 $n$ 个物品， $m$ 个等级。物品 $i$ 从等级 $j - 1$ 升级至 $j$ 需要花费 $a [i] [j]$ ，可正可负，当所有物品均升级至 $k$ 时，会得到 $d [k]$ ，可正可负。
$\;\;\;\;\;$ 求：所能获得的最大值。

$\;\;\;\;\;$ $1\leq n,m \leq 1000$ ， $-10^{9} \leq a_{ij},d_{k} \leq 10^{9}$ .

思路

$\;\;\;$ ~~思路好像比较混乱~~
$\;\;\;$ 将每个物品升级的花费取相反值，转换为获得值。
$\;\;\;$ 最终答案应该是全部物品升级至某一等级（可能为 $0$ ）后，某些物品（ $\rightarrow n-1$ ）再升级至它能获得的最大值。二者的和为最终答案。所以，枚举将全部物品升级至某个等级 $k$ ，再计算出每个物品从当前等级开始，再向后升级能获得的最大值，即 $a [i] [k + 1], . . ., a [i] [m]$ 的最大前缀和。
$\;\;\;$ 从某处向后的前缀和 与 前缀和 的大小关系相同，值不同。
$\;\;\;\;\;$ 前缀和： $b_{1},b_{2},b_{3},...,b_{k},b_{k+1},b_{k+2},...,b_{n}$ .
$\;\;\;\;\;$ 从 $k$ 向后前缀和： $c_{k+1},c_{k+2},...,c_{n}$ .
$\;\;\;\;\;$ 二者的关系： $c_{k+1} = b_{k+1} - b_{k},c_{k+2} = b_{k+2} - b_{k},...,c_{n} = b_{n} - b_{k}$ .
$\;\;\;$ 所以，可以预处理，每个物品的前缀和， $t [i] [j]$ 表示第 $i$ 个物品，从 $j - 1$ 向后的最大的前缀和。也就是说，如果当前枚举至等级 $j - 1$ ，对于第 $i$ 个物品，再向后升级所能获得的最大值为 $t [i] [j] - b [i] [j - 1]$ .
$\;\;\;$ 显然，只有 $t [i] [j] - b [i] [j - 1] > 0$ 时再升级才有效，但是，要记录一下，在全部升级至当前等级下，有多少个物品再升级有效，如果是 $n$ 个物品，就再减去再升级获利最小的那个物品，否则，就是错误的。比如：
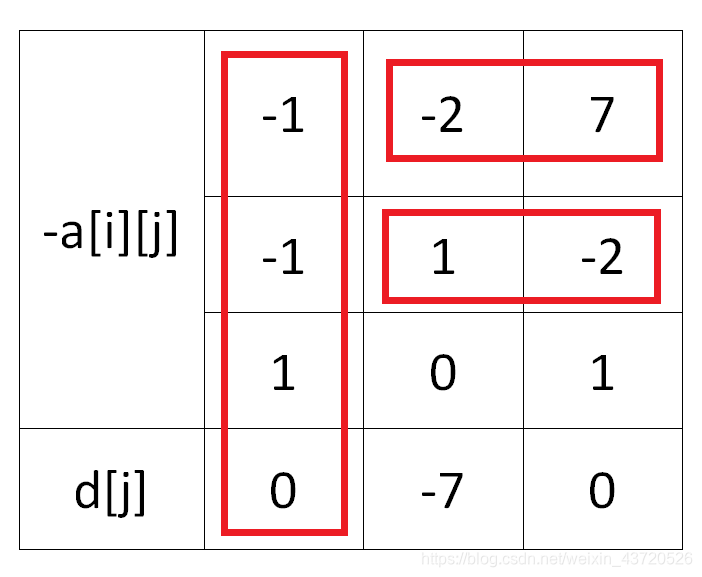
在这里插入图片描述
$\;\;\;$ 最终答案为空框以内，但是枚举至等级 $1$ 时，对于物品 $3$ ，再升级至等级 $3$ 还能获得 $1$ ，但是其升级后相当于将全部物品均升级至等级 $3$ ，与我们当前状态不符。
$\;\;\;$ 时间复杂度： $O (n m)$

代码


#include <bits/stdc++.h>

using namespace std;

const int MAXN = 1005;
#define EPS (1e-10)
#define LL long long
#define INF (1e15)

LL a[MAXN][MAXN], d[MAXN];
LL b[MAXN][MAXN], c[MAXN][MAXN], t[MAXN][MAXN]; 
int main() {
	int T, n, m;
	scanf("%d", &T);
	for(int tt = 1; tt <= T; tt++) {
		scanf("%d%d", &n, &m);	
		memset(b,0,sizeof(b));
		memset(c,0,sizeof(c));
		memset(t,0x80, sizeof(t));
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= m; j++) {
				scanf("%lld", &a[i][j]);
				a[i][j] = -a[i][j];
				b[i][j] = b[i][j-1] + a[i][j]; // ai 的前缀和
				c[i][j] = c[i-1][j] + a[i][j]; // aj 的前缀和 
			}
		}
		for(int i = 1; i <= n; i++) {
			t[i][m+1] = t[i][m] = b[i][m];
			for(int j = m-1; j >= 0; j--) {
				t[i][j] = max(t[i][j+1], b[i][j]);
			}
		}
		for(int i = 1; i <= m; i++) scanf("%lld", &d[i]);
		LL sum = 0, ans = 0;
		for(int i = 0; i <= m; i++) {
			sum += c[n][i] + d[i];			
			LL tmp = 0;
			int cnt = 0;
			LL Min = INF;
			for(int j = 1; j <= n; j++) {
				if(t[j][i+1] - b[j][i]> 0) {
					tmp += t[j][i+1] - b[j][i];
					cnt++;
					Min = min(Min, t[j][i+1] - b[j][i]);
				}
			}
			if(cnt == n) tmp -= Min;
			ans = max(ans, sum + tmp);
		}
		printf("Case #%d: %lld\n", tt, ans);	
	}
	return 0;
}

错误点

$\;\;\;$ 调了好久发现是， $I N F$ 写错了。
$\;\;\;$ 这样写， $I N F = (1 < < 15)$ ，直接溢出。改成（1e15）之后就过了。
$\;\;\;$ 那么最值怎么写呢？
$\;\;\;$ 对于 $i n t$ 型数据，最好写 $I N F = 0 x 3 f 3 f 3 f 3 f$ ，这个值是 $1061109567$ ，也就是 $10^9$ 级别，且 $2$ 倍不会超过 $2147483647$ ，意味着相加不会溢出。
$\;\;\;$ 对于 $long\; long$ 型数据，最好写 $I N F = 0 x 3 f 3 f 3 f 3 f 3 f 3 f 3 f$ ，理由同上。
$\;\;\;$ 整理一下：