线性回归公式推导过程 笔记
线性:
y
=
a
x
y = ax
y=ax 一次方的变化
回归: 回归到平均值
在简单的线性回归中 算法 == 公式
一元一次方程组:
y
=
a
x
+
b
y = ax+b
y=ax+b
一元指的是一个
X
X
X :影响
Y
Y
Y的因素,也指纬度
一次指的是
X
X
X 的变化:没有非线性的变化
做机器学习没有完美解,只有最优解。
如何以最快的速度,找到误差最小的最优解?
利用最小二乘法,求得误差
1
m
∑
i
=
1
m
∣
y
i
^
−
y
i
∣
\frac{1}{m}\sum_{i=1}^{m}\vert\widehat{y_{i}}-y_{i}\vert
m1∑i=1m∣yi
−yi∣
找到误差最小的时刻,为了去找到误差最小的时刻,需要反复尝试 a , b 根据最小二乘法求得误差。
反过来,误差最小时刻的 a , b 就是最终最优解。
多元线性回归
本质上就是算法(公式)变为多元一次方程组。
y
=
w
0
x
0
+
w
1
x
1
+
w
2
x
2
+
w
3
x
3
+
.
.
.
+
w
n
x
n
y=w_{0}x_{0}+ w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+...+w_{n}x_{n}
y=w0x0+w1x1+w2x2+w3x3+...+wnxn
=
w
T
x
=w^{T}x
=wTx
数据随机抽取,大部分会遵循正态分布。
做回归 == 做拟合
目标函数 RMSE(代价函数、损失函数 cost function)
R
=
R
o
o
t
开
根
号
,
M
=
M
e
a
n
均
值
,
S
=
S
q
u
a
r
e
d
平
方
,
E
=
E
r
r
o
r
误
差
R=Root_{开根号}, M=Mean_{均值}, S=Squared_{平方}, E=Error_{误差}
R=Root开根号,M=Mean均值,S=Squared平方,E=Error误差
MSE 越小,model 越好
最大似然估计(maximum likelihood estimation, MLE)
最大似然估计是一种统计方法,它用来求一个样本集的相关概率密度函数的参数。
“似然”:Likelihood 可能性,最大可能性估计
中心极限定理 (central limit theorem)
是指概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。
假设 A , B 事件独立:
P
(
A
B
)
=
P
(
A
)
P
(
B
)
P(AB) = P(A)P(B)
P(AB)=P(A)P(B)
∏
i
=
1
m
=
P
(
X
i
)
\prod_{i=1}^{m}=P(X_{i})
∏i=1m=P(Xi)
最
大
总
似
然
⟹
最
小
M
S
E
最大总似然\Longrightarrow 最小MSE
最大总似然⟹最小MSE
概率密度函数
而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。
当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。
正态分布的概率密度函数:
f
(
x
)
=
1
2
π
e
−
(
x
−
μ
)
2
2
δ
2
f(x)=\frac{1}{\sqrt[]{2\pi}}e^{-\frac{(x-\mu)^2}{2\delta^2}}
f(x)=2π1e−2δ2(x−μ)2
随
着
μ
和
δ
变
化
,
概
率
分
布
也
产
生
变
化
随着\mu和\delta变化,概率分布也产生变化
随着μ和δ变化,概率分布也产生变化
公式推导过程
前提:1.随机(服从正态分配)2.独立(认为误差是独立的)
把公式中的误差带入概率密度函数:
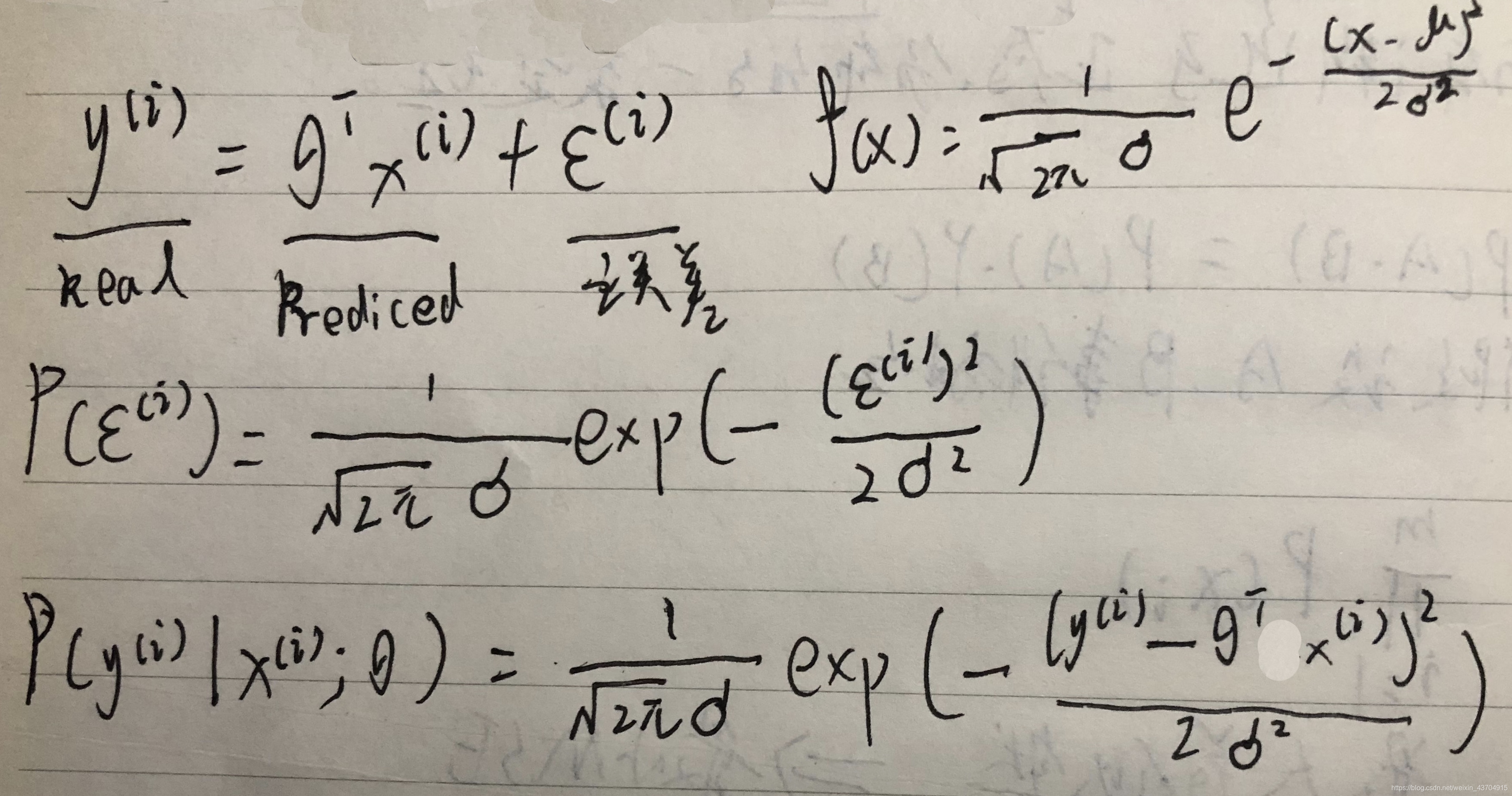





























 2040
2040

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








